Jérôme de Lalande - Astronomie (ed.1764)
J’ai eu l’opportunité de pouvoir réunir ces deux volumes de l’édition originale de 1764 de Astronomie de Jérôme De La Lande. Cet ouvrage est la synthèse des cours que donnait l’astronome au Collège de France.
"Astronomie" est considéré comme une œuvre de référence qui surpassait les autres publications de son époque. Il fut diffusé dans plusieurs pays et contribua à former des générations d’astronomes. Cet ouvrage fit l’objet de multiples rééditions ou compléments. La dernière édition de 1781 comportait quatre tomes.
Les biographes ont décrit Jérôme De La Lande comme une personne originale, aux comportements parfois bizarres. Ils citent de manière anecdotique qu’il lui arrivait de gober des araignées, pour guérir de leur phobie ceux qui ne pouvaient supporter leur vue. Il n’en fut pas moins un brillant érudit et un infatigable travailleur qui professa au Collège de France pendant quarante six années et qui compta parmi ses élèves, Delambre ou Mechain.
Avec Lalande, nous abordons des textes d’une grande rigueur, car l’auteur est un véritable scientifique, bien que certains de ses ouvrages moins connus révèlent également des talents d’écrivain. Lors de mes recherches sur Lalande, j’ai eu l’occasion d’entrer en contact avec Laurence Bobis*, directrice de la bibliothèque de l’Observatoire de Paris, qui m’a mis en relation avec Simone Dumont, auteur d’un ouvrage intitulé : " Un astronome des lumières Jérôme Lalande " (Ed. Vuibert 2007). Cette dernière m’a renseigné sur les méthodes de travail de l’astronome, quand à la rédaction du livre que je présente ici. Dans un courrier, elle m’écrit: « Cette Astronomie est le premier grand ouvrage de Lalande qu’il complètera à chaque nouvelle édition. Il a demandé à ses lecteurs de lui communiquer toutes les erreurs qu’ils pourraient trouver ou toute autre remarque... » Ainsi Jérôme de La Lande est particulièrement attaché à l’exactitude de ce qu’il rédige. Il y fait d’ailleurs allusion en ces termes: « Quelque envie que j’eusses de diminuer la sècheresse d’une étude si ennuyeuse, l’exemple de M. de Fontenelle ne m’a point séduit. Je n’ai osé n’y mêler ni dialogue ni épisode, ni digression. Le goût épuré de notre siècle semble avoir écarté cette manière enjouée de présenter les sciences. »
* Laurence Bobis a quitté la direction de la bibliothèque de l'observatoire. Elle est actuellement ( mars 2017) directrice de la bibliothèque universitaire de la Sorbonne.
Lalande met en garde sur le « désordre des passions ». Selon lui, la connaissance n’est pas une fin en soi, en ce sens que seul celui qui parvient à penser par lui-même peut développer son esprit. Ce propos caractérise la réflexion qui domine chez les scientifiques en ce milieu du siècle des lumières. Lalande écrit encore: « Le sage s’élève avec raison contre ceux que l’admiration des astres a portés jusqu’à en faire des Dieux; mais bien loin d’en condamner l’étude, il la conseille pour la gloire du Créateur. » Un tel propos laisse planer le doute; Lalande était t’il croyant ou athée? Du Pont de Nemours, dans l’éloge funèbre qu’il prononce aux obsèques de l’astronome ne déclara t’il pas: « Il était plus religieux qu’il ne croyait l’être, puisqu’il s’est montré constamment homme de bien, rempli d’honneur, de probité de courage, d’activité pour toutes les choses utiles, d’amour et de zèle pour le genre humain » Lalande par ailleurs ayant écrit: « je crois la vertu d’un athée plus sure et plus noble que celle d’un croyant... L’équité est le soutien du genre humain... la bonté enchaine tous les cœurs... » ce qui laisse envisager une certaine capacité à s’affranchir des croyances.
Il est légitime pour un professeur d’astronomie d’indiquer à ses élèves comment se procurer du matériel d’observation. Ici, Lalande dresse quasiment un catalogue avec les prix et les principales caractéristiques des instruments disponibles chez divers marchands. La première lunette de six pieds dont il est question ici coute quatre vingt seize livres. A titre indicatif, le salaire journalier d’un compagnon maçon à la fin du XVIIIème siècles est d’environ une livre et dix sols ( 1,5 livre). Ramené à nos jours, le prix d’une telle lunette avoisinerait trois mille euros, ce qui correspond approximativement à l’équivalent de deux mois de salaire d’un employé. On peut en déduire que l’acquisition d’un tel instrument n’était certainement pas à la portée d’un étudiant de condition modeste vivant au XVIIIème siècle.
Lalande débute son ouvrage par un énoncé des fondamentaux de sa discipline. En fait, il s’agit là d’une description des mouvements apparents de tous les astres, tels qu’on peut les observer depuis la Terre. L’auteur développera ainsi les principes de la sphère en donnant de manière exhaustive toutes les caractéristiques que l’on peut déterminer, comme la longitude et la latitude géographique d’un lieu, mais aussi l’obliquité de l’écliptique, les heures de lever et coucher du Soleil etc... Mon propos n’est pas ici de reprendre son cours, qui remplit plus de mille cinq cent pages, illustrées de plusieurs centaines de figures, mais bien de lever le voile sur quelques aspects de la teneur d’un livre considéré lors de sa parution comme la «Bible » de l’astronomie.
Cet extrait montre que Lalande, tout en étant précis dans son énoncé, ne se prive pas de donner quelques conseils, montrant qu’il est aussi un observateur avisé. Il faut savoir que vers l’âge de seize ans, lorsqu’il a quitté sa vile natale, Bourg en Bresse, pour commencer des études de droit à Paris, il logeait dans une soupente de l’hôtel de Cluny qui disposait d’une « tour-escalier » au sommet de laquelle l’astronome, académicien et professeur au Collège de France, Joseph Nicolas Delisle avait installé son observatoire personnel. Ce dernier invita d’ailleurs le jeune Lalande dans cet observatoire et, dés 1749, commença à l’instruire sur les techniques d’observation ainsi que sur l’astronomie théorique.
A l’issue d’un premier volet descriptif, Lalande propose d’envisager l’astronomie à travers ses origines et son histoire. Ici encore l’érudition de l’auteur ne peut que laisser admiratif. Après avoir abordé les aspects mythologiques de l’astronomie et évoqué son importance chez les Chaldéens, il traite ici de l’astronomie égyptienne. Lalande attribue à ce peuple la première idée du mouvement de la Terre ou du système Copernicien, qu’Aristarque reprendra par la suite pour le diffuser auprès des grecs. Il leur attribue également d’avoir imaginé, les premiers, l’idée de pluralité des mondes qui séduira à son tour Pythagore qui, ne l’oublions pas, avait effectué un long séjour à Thèbes en Égypte durant son initiation.
Ce passage nous éclaire sur le rôle que jouèrent les arabes (alors nommés Sarrasins), pendant plus de cinq siècles, en des temps où notre civilisation occidentale stagnait dans l’obscurantisme. Au terme de son exposé et après avoir mis en avant les contributions de Al Mamun, Albategnius, Alfragan, Alhazen… il évoque l’œuvre d’Ulugh Beg « Le grand ouvrage de ce prince est son catalogue d’étoiles, dressé à Samarkand l’an de l’hégire 841 ou 1437 de JC... » il mentionne également que: « Les tables astronomiques pour le méridien de Samarkand... étaient si exactes qu’elle différaient peu de celle de Tycho Brahé »
L’astronomie chinoise ne fut jamais considérée très sérieusement par les occidentaux. Lalande en souligne quelque aspects, relatés dans un livre du Père Antoine Gaubil (1689-1759), missionnaire jésuite qui avait étudié l’astronomie au cours d’un séjour en Chine qui dura près de trente années. Ce religieux officiait comme interprète à la cour de l’empereur Yong Zheng (1678-1735,) que Voltaire comparait à Louis XIV en le qualifiant de « despote éclairé ». Le père Gaubil occupa également des fonctions similaires pour l’empereur Qianlong (1711-1799). J’aurais l’occasion de revenir sur l’astronomie chinoise en produisant des extraits de ce livre du père Gaubil, dont je possède une édition, reliée au sein d’une compilation nommé Lettres édifiantes et curieuses, publiée au début du XIXème siècle.
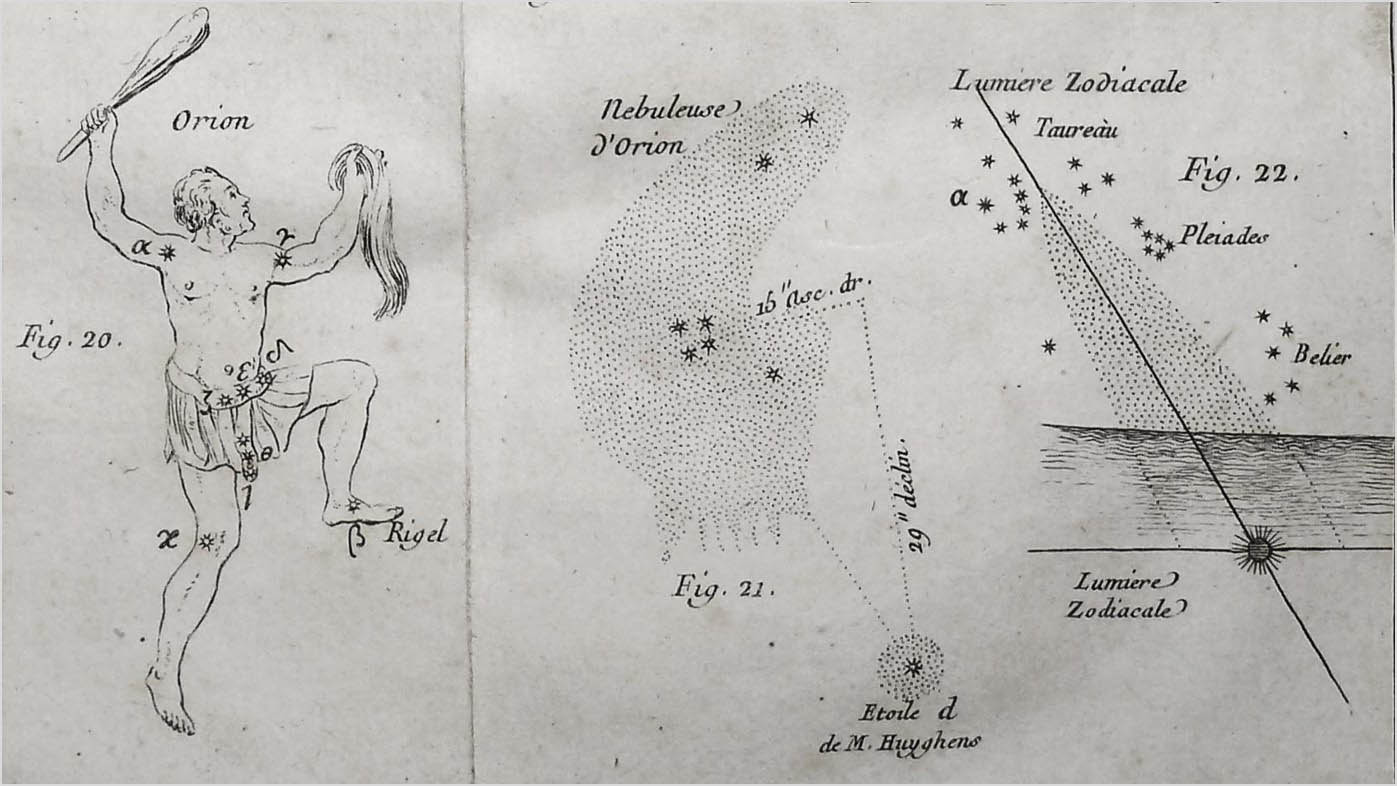
Après avoir retracé l’histoire de l’astronomie « occidentale » jusqu’à son époque, Lalande ouvre un troisième livre pour y traiter des étoiles fixes et des constellations dont il donne la définition suivante: « Les constellations sont des figures qu’on imagine dans le ciel, pour rassembler sous un nom commun un certain nombre d’étoiles: cette méthode en facilite l’étude et en rend même l’usage plus commode ». Dans l’extrait ci-dessus, Lalande donne une méthode pratique qui permet d’identifier les principales étoiles et de les rattacher à leur constellation ou à une constellation voisine.
Dans le texte concernant le dessin de la nébuleuse d’Orion, on trouve ce commentaire de Lalande: « J’ai donné dans la fig.21 le dessin de cette nébuleuse, d’après Monsieur de Mairan: on y voit l’étoile de M. Huyghens, environnée d’une nébulosité de même espèce ». Mairan avait décrit cette singularité, dès 1731, en ces termes: « nébulosité brillante entourant une étoile... très similaire à l'atmosphère de notre Soleil, si elle était assez dense et étendue pour être visible dans des télescopes à la même distance ». Lalande ne se doutait pas que la nébulosité en question serait connue, de nos jours, sous le non de « Nébuleuse de Mairan* » ou M43 dans le catalogue Messier.
*Jean Jacques Dortous de Mairan était un mathématicien et astronome, admis à l’Académie des Sciences en 1718, et qui en devint le président après le départ de Fontenelle. Il fréquentait les salons mondains et entretenait une correspondance régulière avec les savants et les érudits de toute l’Europe.
Fait assez exceptionnel, ces deux pages comportent dans leurs marges des annotations manuscrites qui pourraient laisser penser qu’il s’agit là de l’écriture d’un de ces lecteurs auxquels Lalande envoyait ses ouvrages, afin de recueillir remarques ou suggestions. En effet l’exemplaire en ma possession possède plus d’une cinquantaine de ces notes ou croquis manuscrits. Les descriptions simples mais précises des constellations nous indiquent que ces figures ne sauraient être décrites de la sorte que par un observateur aguerri.
Ces planches montrent un échantillon des multiples figures qui illustrent les démonstrations géométriques et trigonométriques de l’ouvrage. On y reconnaitra (fig.45,46,47,48) les différentes représentations, géocentriques ou héliocentriques, du monde.
Généralement, les scientifiques des Lumières n’ont jamais porté les astrologues en très haute estime. Une partie des ouvrages d’astronomie de l’époque y fait en effet référence en des termes sans équivoque. Lalande pose également son regard critique sur l’astrologie. Il isole le contenu astronomique pour en extraire quelques éléments; sans pour autant épargner ceux qui seraient susceptibles de lui attribuer une quelconque valeur prédictive. Le commentaire sur les motivations d’un certain «Grand Seigneur », désireux de consulter tous les ouvrages d’astronomie issus de l’Académie des Sciences, est on ne peut plus évocateur des croyances qui affectaient, jusqu’au plus haut niveau, les dignitaires de l’état. Notons que la Guerre de sept ans venait de faire perdre à Louis XV (probablement « sa Hautesse », dont il question dans cet extrait) un grande partie de ses possessions coloniales, au profit des Britanniques.
Une cinquantaine de pages de cet ouvrage est consacrée à la description des seuls mouvements de la Lune. Comme je l’ai déjà évoque brièvement, les mouvements qui animent cet astre sont très complexes. Lalande recense ici les quatre irrégularités principales qu’il nomme: « l’équation du centre, l’évection, la variation et l’équation annuelle ». Il note également une accélération du « moyen Mouvement de le Lune » qu’il nomme « équation séculaire ». Dans cet extrait, il reprend les mesures effectuées par différents astronomes. Il refermera ce chapitre en commentant: « Le calcul de l’attraction a fait voir beaucoup d’autres inégalités sensibles dans les latitudes de la Lune, mais elles sont assez petites pour qu’on puisse les négliger... »
Lalande aborde maintenant la parallaxe du Soleil en commençant par retracer l’historique de cette méthode de mesure des distances. À la suite de cet extrait, il donne la distance du Soleil à la Terre, issue de la mesure de parallaxe moyenne, effectuée à six mois d’intervalle (d’avril à octobre), qui s’établit à 9’’. Il commente: « La parallaxe du Soleil étant connue, sa distance absolue est aisée à trouver, car le sinus de 9’’ est au rayon, comme le demi diamètre de la Terre est à la distance du Soleil, et comme le rayon d’un cercle est 22 918 fois plus grand que le sinus de 9’’, il s’en suit que la distance du Soleil est de 22 918 fois le rayon de la terre, ou environ 33 millions de lieues communes de France de 2282 toise ». Soit une distance de 147,477 millions de km, ce qui correspond à moins de 1,5 % d’erreur par rapport aux 149,598 millions de km réels (base de l’unité astronomique de distance: ua ).
Déterminer les phases d’une éclipse, nécessite de fastidieux calculs. Le croquis ci-dessus montre comment les déterminer plus simplement « avec la règle et le compas » (pour reprendre les propres mots de l’auteur). À titre d’exemple, voici un commentaire de Lalande: « On voit dans la fig.116 les diamètres des ellipses qu’on trouverait pour différentes déclinaisons en employant le même rayon de projection. La fig.115 fait voir à quelle distances passeront toutes ces éclipses du sommet S de la projection, c’est-à-dire, la distance SK. On voit au milieu de la fig.114 les lieux des centres de ces différents ellipses; Chacun pourra les tracer toutes sur autant de cartons différents, pour calculer les éclipses de toutes les étoiles par la Lune. Pour rendre l’usage de cette méthode plus facile, je donnerai dans les mémoires de l’académie pour 1763 des ellipses pour tous les degrés de déclinaison, dont l’échelle sera double de celle de la fig.114, et qui seront divisées exactement de 5 en 5 minutes ... »
L’observation des passages de Mercure ou de Vénus entre la Terre et le Soleil ne fut possible qu’après l’invention de la lunette. Lalande souligne ici l’importance de tels évènements pour la connaissance des distances astronomiques. Edmund Halley fut le premier à mettre au point une méthode de calcul permettant de connaitre les dimensions du système solaire. Auparavant, Kepler avait donné les proportions entre les distances séparant les planètes, sans pour autant pouvoir établir une valeur absolue. Dans un tableau, Lalande reprend dix sept résultats d’un calcul de Halley concernant les passage de Vénus devant le Soleil. Ces calculs ont été corrigés par M. Trébuchet (1722-1784), calculateur recruté par Lalande pour la Connaissance des Temps, car Halley n’avait pas pris correctement en compte le mouvement du nœud de Vénus, fort peu connu à son époque. On note, répertorié ici, un transit de Vénus prévu plus de 240 années à l’avance, soit le 7 Juin 2004. Ce transit a bien eu lieu, avec seulement une douzaine d’heures de retard et une parallaxe équatoriale de 8’66’’, proche à 36’’ prés de la prévision.
Cette figure permet de repérer les différentes zones du globe à partir desquelles une éclipse est visible. Lalande commente: « Pour tracer sur la mappemonde ces cercles d’entrée et de sortie, il faut encore y marquer le cercle d’illumination au moment de l’entrée, et au moment de la Sortie, vues du centre de la Terre; car ces ligne FGB, BAD,EGH, CAI marqueront tous les points où l’on doit voir l’entrée et la sortie au moment du lever ou du coucher du Soleil et serviront par conséquent de limite... Il s’agit maintenant de tracer les cercles d’entrer et de sortie pour 7h17’, 20’, 23’, 26’ afin de connaître les pays où l’effet de la parallaxe sera le plus considérable, et de pouvoir choisir en conséquence la position la plus favorable pour l’observer... Ayant tracé tous les cercles d’entrée et de sortie dans le passage de 1769, j’ai vu que l’entrée à Mexico dans la nouvelle Espagne sera à 7h 21’10’’, la sortie à 13h37’40’’; ainsi la durée totale du passage y sera de 6h 16’30’’... ainsi deux observations complètes de ce passage en 1769, dont l’une serait au Mexique et l’autre au nord de Petersbourg, nous donneraient avec une précision deux fois aussi grande que celle du dernier passage observé en 1761, la parallaxe du Soleil ». Lalande fut chargé, cinq ans après la sortie de ce livre, de centraliser la campagne française qui connu malheureusement de nombreux déboires. Pingré fut envoyé à Saint Domingue, Le Gentil dans l’Océan Indien et Chappe d’Auteroche, qui avait déjà observé l’éclipse de 1761 en Sibérie, s’était rendu, cette fois, en Basse Californie, où il mourut trois jours après le passage de Vénus.
Au fur et à mesure de l’évolution de leurs instruments, les astronomes effectuent des mesures de plus en plus précises. Cet accroissement de la précision rend nécessaire la prise prendre en compte, dans leurs calculs, d’éléments correctifs comme, par exemple, ceux relatifs à la réfraction atmosphérique. Ce phénomène consiste en une déformation de la trajectoire de la lumière lorsqu’elle traverse l'atmosphère. Cette déformation est due à la variation de la densité de l'air en fonction de l’altitude. La prise en considération et la correction de la réfraction astronomique permettait, à partir du relevé de la position angulaire apparente de l'astre observé, d’obtenir un résultat indiquant sa position réelle.
L’astronome du XVIIème siècle a vu la naissance des instruments optiques, celui du siècle suivant se préoccupera de leur amélioration. Ici Lalande traite de la qualité du verre des lentilles, relativement à l’aberration chromatique. Comme je viens de le mentionner, la précision des instruments de mesure couplés aux instruments d’observation, ne pouvait plus s’accommoder d’imperfections qui restaient tolérables en visuel. Ainsi le chromatisme, que généraient les lentilles en verre ordinaire, devenait un véritable problème. On comprend à cette occasion, en quoi les différentes disciplines que réunie l’astronomie sont devenues interdépendantes, dans le sens où les avancées des unes imposèrent aux autres de multiples tâtonnement et travaux de recherches. On peut aussi imaginer, à ce titre, l’effervescence qui devait régner alors dans les milieux scientifiques.
De nos jours, lorsqu’on achète un télescope ou une lunette, l’instrument est accompagné de nombreuses mises en garde contre les dangers relatifs à l’observation du Soleil. Au XVIIIème siècle le risque était identique et la négligence des observateurs pouvait aussi entrainer de graves accidents. Lalande fait ici un rappel sur le bon usage des instruments. Dans ce même chapitre il évoque aussi l’utilisation des filtres colorés: « quelques astronomes se servent de morceaux plans de verre colorés en rouge, en jaune, en bleu ou en vert; mais on doit craindre l’irrégularité qu’il y a presque toujours dans la matière et dans l’épaisseur de ces sortes de verres: on aperçoit des défectuosités monstrueuses quand on met ces verres sur l’objectif, comme M. Le Gentil l’a éprouvé, au lieu que l’on a facilement des morceaux de glace que l’on peut enfumer et que l’on éprouve en les plaçant sur l’objectif de la lunette, sans que le Soleil cesse de paraitre bien déterminé... »
Lalande produit ici un texte de Sénèque, philosophe romain, né à Cordoue en l’an 3 de notre ère. Ce dernier fut précepteur de Néron avant de devenir un de ses principaux ministres. Le philosophe finit par incommoder le tyrannique empereur dans ses sombres projets. Son rôle de censeur conduisit Néron à le condamner à mort. Le 12 avril 65, Sénèque prit les devants en demandant qu’on lui tranche les veines. Ce philosophe écrivit peu sur l’astronomie, cependant dans son livre Questions naturelles, il émit quelques idées marquant son génie, comme l’extrait ci-dessus le laisse apparaître.
Lalande restitue un texte de Galilée qui fut le premier à mettre en évidence ce qu’il nomma la libration de notre satellite. Cette libration fut également analysée en détail par Lalande qui fit apparaitre qu’elle se compose de quatre mouvements d’origines distinctes. La libration diurne ou parallactique, très faible, d'un degré environ. La libration en latitude, provenant de l'inclinaison de l'axe de la Lune sur l'écliptique. La libration en longitude, provenant des inégalités du mouvement de la Lune dans son orbite et enfin, la libration provenant de l'attraction terrestre sur la sphéroïde lunaire. Les deux premières librations avaient déjà été reconnues par Galilée, la troisième fut identifiée par Hevelius et Riccioli enfin la quatrième fut mise en évidence par Newton.
La lunette astronomique permit à Christian Huygens de découvrir l’anneau de Saturne. Dans cet extrait, Lalande recense quelques interprétations erronées qu’en firent les astronomes, avant de donner une véritable explication de la nature de ces anneaux, si ce n’est que concernant leur épaisseur, rien n’était alors définitivement tranché. Lalande précise : « On remarque sur le globe de Saturne des bandes semblables à celles de Jupiter, mais beau coup plus faibles... M. Cassini ne put apercevoir sur le globe de Saturne aucun point remarquable dont le mouvement pût faire distinguer la rotation de Saturne; nous sommes donc à cet égard dans la même position que par rapport à Mercure, et nous ignorons même si Saturne a un mouvement sur son axe ».
Lalande ne saurait se soustraire à l’évocation de la pluralité des mondes. Compte tenu cependant de la densité de son ouvrage Astronomie, on pourra regretter qu’il consacre si peu de place à cette question qui exaltait les esprits les plus féconds de son époque. Il résume pourtant en peu de mots, l’essentiel de ce qui pouvait alors être dit sur le sujet, laissant semble t-il à d’autre le soin de s’étendre en conjectures. Les biographes de Lalande révèleront d’ailleurs un homme plutôt discret quand à ses convictions intimes et qui, à l’opposée, se montrait parfois extravagant lorsqu’il se donnait en spectacle et cultivait des attitudes provocatrices, qui lui donnaient l’occasion de se délecter du regard des autres.
Lalande consacre plusieurs paragraphes à l’arithmétique des infinis qui était une branche utile aux géomètres. La grande encyclopédie Diderot-d’Alembert la définie ainsi: « L’Arithmétique des infinis est la méthode de trouver la somme d’une suite de nombres dont les termes sont infinis, ou d’en déterminer les rapports... M. Wallis est le premier qui ait traité à fond de cette méthode, ainsi qu’il parait par ses Opera mathematica, où il en fait voir l’usage en Géométrie, pour déterminer l’aire des surfaces... ». Cet outil était utilisé dans le calcul des forces d’attraction exercées par les planètes et ainsi, il rendait possible le rapprochement entre ces forces et les inégalités de trajectoire de la Terre ou d’autres planètes. Par exemple devenait t-il possible de calculer l’incidence de Jupiter sur la Terre ou d’établir une théorie de la Lune à l’usage de la navigation, comme Lalande, Clairaut ou La Caille s‘y employèrent.
Au XVIIème siècle, Pierre de Fermat, Blaise Pascal et René Descartes introduisent l’usage de l’algèbre en géométrie, ce qui ouvrit un porte à la géométrie analytique. Ainsi, les droites, les courbes ou les surfaces peuvent être définies par des équations dans un repère donné et positionnées au sein de ce repère grâce à leurs coordonnées. Apparait alors l’intérêt que peut en tirer l’astronomie. Le calcul différentiel fait partie des outils de « l’arithmétique des infinis » telle que la décrit Lalande à la page précédente; on attribue son invention à Newton et à Leibnitz. Il se nommait alors « méthode des fluxions » et entrait dans les calculs qui permettaient la traduction de mesures astronomiques en lois mathématiques.
Dés qu’il est question d’aires ou de volumes, définis par des fonctions mathématiques, intervient le calcul intégral que Lalande définit comme « l’inverse du calcul différentiel ». Il cite: « Le calcul intégral sert à trouver la cubature* des solides, aussi bien que la quadrature** des courbes... le seul usage que nous en fassions en astronomie consiste à trouver la solidité, ou le volume de la Terre, en la supposant produite par la rotation d’une ellipse autour de son petit axe. Un sphéroïde tel que la Terre est égal aux deux tiers du produit de son grand axe par la surface du méridien ou de l’ellipse génératrice. »
* La cubature (ou cubage) d'un solide, est l’évaluation algébrique ou numérique de son volume.
** La quadrature d’une courbe est l’évaluation de la surface quelle sous-tend.
Les méthodes générales permettant la cubature des volume ou la quadrature des courbes comptent parmi les applications majeures du calcul intégral.
Après avoir assez longuement commenté les outils mathématiques exploitables par les astronomes aguerris, l’auteur revient ici à des considérations plus pratiques. Il introduit l’utilisation des logarithmes, particulièrement utiles, dés qu’il s’agit de faire des opérations de calcul avec des nombres de très grande valeur. Le logarithme permet en effet de transformer un produit en somme. Ainsi multiplier des nombres revient à additionner leur logarithmes. La seule contrainte réside dans l’utilisation de tables de correspondance nombre/logarithmes. En 1802, Lalande publiera d’ailleurs une table de logarithmes, calculés avec cinq décimales et pour les nombres de 1 à 10.000, ainsi qu’une table des logarithmes des sinus et des tangentes calculés de minutes en minutes de 0° à 90°. Ces tables seront, plus tard étendues à sept décimales par le Baron Raynaud et utilisées jusqu’à l’apparition des calculatrices électroniques et de l’informatique.
Les interpolations, sont un prolongement des logarithmes, qui permet d’éviter la lourdeurs de calculs à partir de fonctions algébriques complexes. Le principe est une évolution de l’utilisation des logarithme. Par exemple, lorsqu’on dispose d’éphémérides donnant les positions d’un astre donné ou tout autre grandeur relative à cet astres, pour des intervalles réguliers dans le temps, l’interpolation permet d'évaluer la position de cet astre à des moments intermédiaires de ces intervalles, non fournis par les éphémérides. Par exemple si l’on connait la position d’une planète pour un jour et son lendemain à la même heure, l’interpolation permet de trouver la position de cette planète à n’importe quelle heure comprise dans l’intervalle donné. L’interpolation se fait en considérant que durant l’intervalle dans lequel se situe le moment concerné, la variation de la fonction même définissant la position de l’astre en question est négligeable ou que la fonction est assimilée à une fonction linéaire sur cet intervalle.
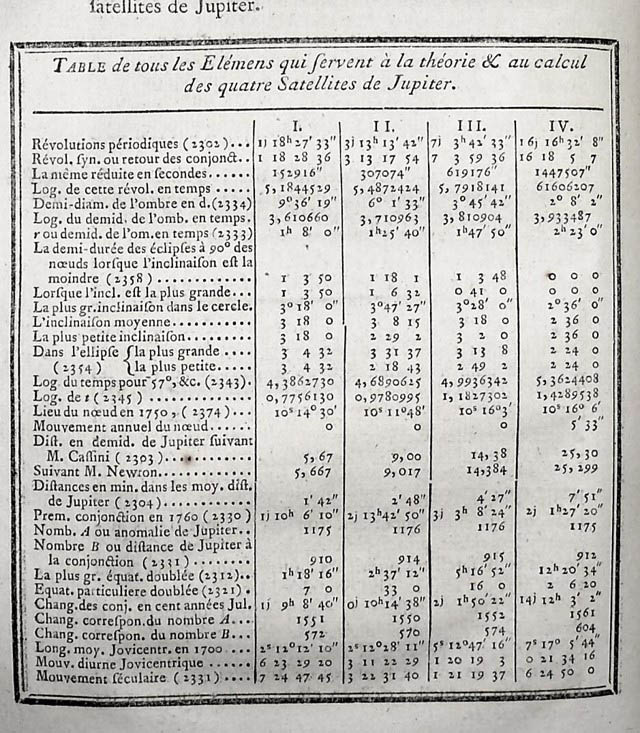
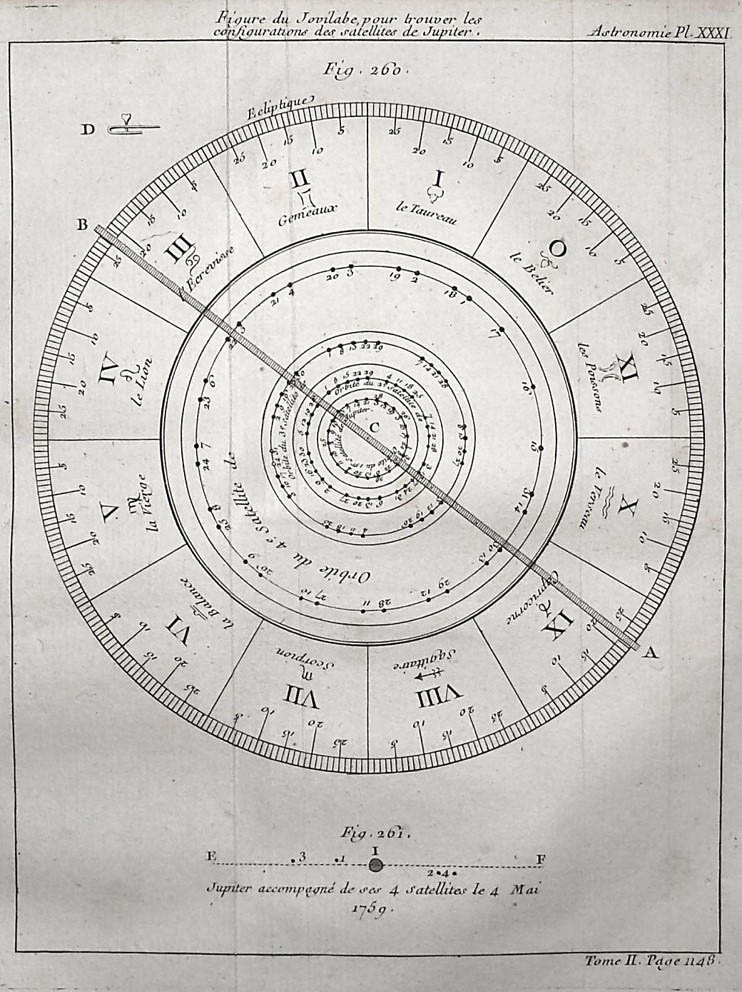
Cette figure ci-dessus montre le principe du «Jovilabe » dont se servait l’astronome Maraldi. Cet instrument inventé par Galilée permettait de déterminer la position des satellites de Jupiter à un moment donné. Lalande travaillera lui-même sur une théorie des satellites joviens prenant en considération les lois de la gravitation, ainsi qu’un bon nombre de données comme le fait apparaître le tableau ci-dessous. En mesurant les moments précis des immersions ou des émersions des satellites de cette planète, les astronomes pouvaient alors déterminer les différences de longitudes entre les lieux depuis lesquels ils observaient le ciel.
« La règle AF étant fixée en F, et dans une situation verticale au moyen d’un fil à plomb, on dirigeait les pinnules O, L, du côté d’un astre, et les divisions de la règle GD qui avait environ six pieds, marquaient la corde de l’angle GAD qui était la distance de l’astre au zénith, ou le complément de la hauteur méridienne »
Ce qui fera écrire à Lalande dans son livre "Astronomie des dames": « Toute l’astronomie est fondée sur la mesure des angles ». Quelques siècles plus tard, il en était encore de même. John Flamsteed entreprit d’effectuer des observations de précision. Comme il ne put se procurer un quart de cercle mural, il utilisa le sextant représenté sur la gravure ci-contre. Malheureusement, il ne put en tirer grand profit. Lalande nous en parle en ces termes: « Avant que ce sextant mobile fut construit, Flamsteed avait demandé qu’on fit faire un quart de cercle pour mesurer les hauteurs méridiennes des étoiles, on le lui avait promis ;mais un des Membres de la Société Royale ayant voulu le faire construire à sa manière, il se trouva hors d’état de servir, et Flamsteed se tourna du côte de l’observation des distances; dans le même temps qu’à l’Observatoire Royal de Paris on observait les hauteurs méridiennes des astres.... Flamsteed essaya d’observer les hauteur méridiennes avec le sextant... mais comme cela était fort difficile, il fit construire à ses frais en 1683 un instrument du même rayon, qu’il divisa lui-même, et dont il se servit plusieurs années ». La longueur du rayon du sextant de Flamsteed était de 6 pieds 9 pouces ¼, en mesure anglaise, ce qui correspond à environ 1,82 m. Son utilisation fastidieuse nécessitait de monter sur un escabeau pour effectuer chaque visée.
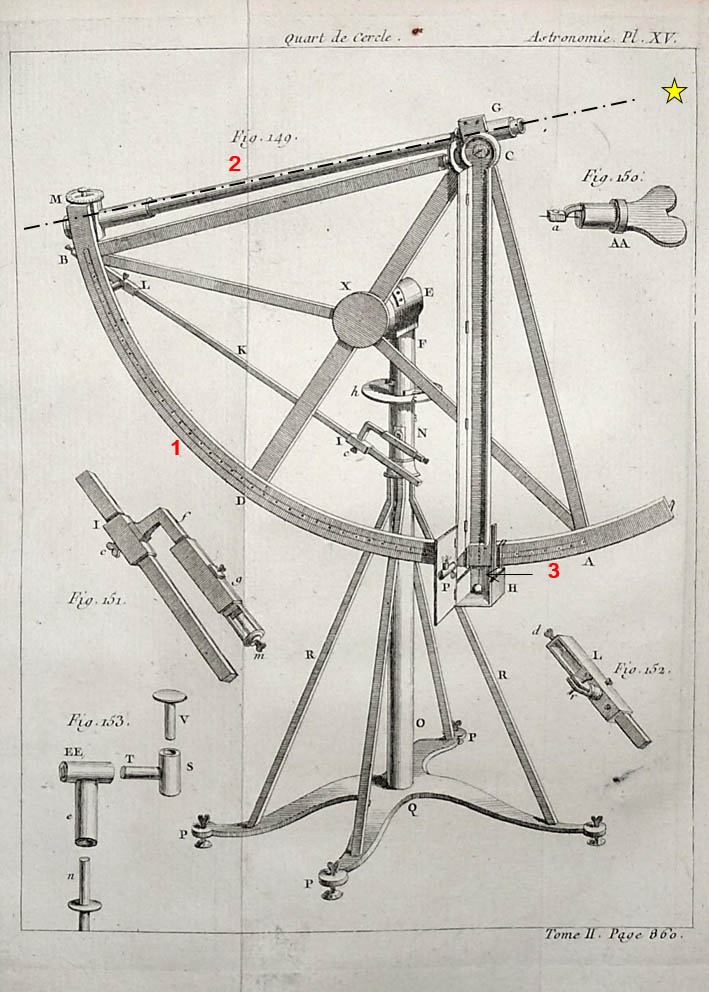
« Le quart de cercle mobile est de tous les instruments d’astronomie, celui dont l’usage est le plus ancien, le plus général, le plus indispensable, le plus commode... » tels étaient les commentaires de Lalande. (Ci-contre le quart de cercle de Tycho Brahé vers 1580).
On attribue l’invention de cet instrument nommé aussi quadrant, à Al Khawarizmi qui vécut à Bagdad au IXème siècle.
Le quart de cercle était utilisé à son origine pour la détermination de l’heure des prières, à partir de l’observation des étoiles ou du Soleil. Constitué d’un limbe (1) gradué de 0 à 90°, il permet de mesurer l’angle que fait la direction d’un objet céleste avec la verticale du lieu d’observation. Pour cela, on vise une étoile avec la lunette (2) et la verticale est obtenue à l’aide d’un fil à plomb (3) dont on lit la position sur la graduation du limbe. Doté d’un axe vertical et d’un axe horizontal, il permet de pointer dans toutes les directions.
La précision de l’angle mesuré dépend en partie de la qualité de lecture du fil à plomb sur les divisions du limbe. Lalande décrit le montage: « Autour du cylindre qui porte le quart-de-cercle, il y a une plaque de cuivre plus large, ronde, fixée sur la charpente de l’instrument. Sur cette pièce est suspendu le garde-filet (CH); c’est une longue boite de cuivre, mince, soutenue vers le centre, autour duquel elle tourne pour se mettre toujours à l’aplomb, et contenir le fil ou le cheveux qui pend du centre pour marquer la division. Ce garde fil a une porte qui se ferme avec deux petits crochets, pour garantir mieux le fil de l’agitation de l’air; on la voit ouverte sur la gauche dans la fig.149; il porte à sa partie inférieure (H) une autre boite plus large, dans laquelle on loge un vase plein d’eau. Le poids qui tend le fil plonge dans cette eau, pour que ses vibrations soient plus tôt arrêtées; cette boite a une porte (P) où est attaché un microscope et une lampe à deux mèches, la lampe sert à éclairer le limbe et le fil à plomb pour voir sur quelle division il répond; le microscope sert à grossir les points pour mettre facilement et exactement le fil du quart-de-cercle sur tel point que l’on veut. »
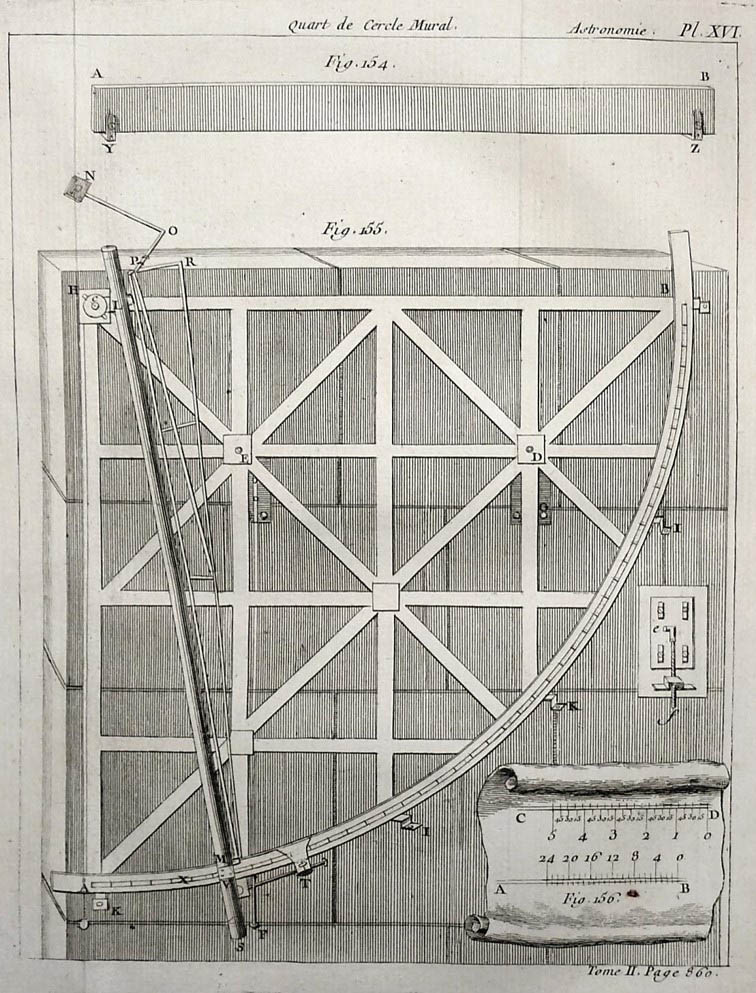
Le quart de cercle mural, ci-contre, a sa propre histoire. Fabriqué à Londres par Jonathan Sisson en 1742, il fut installé en 1743 dans l’observatoire de Pierre Charles Le Monnier, rue Saint Honoré à Paris. Jérôme de Lalande initialement étudiant en droit, est poussé par Louis Nicolas Delisle à étudier l’astronomie. Il assiste aux cours que donne Le Monnier, alors titulaire d’une chaire de Physique au Collège Royal. Devenu un de ses élèves favoris, Lalande est envoyé à Berlin par l’éminent professeur, afin d’y effectuer des mesures sur la parallaxe de la Lune.
C’est à cette occasion que Le Monnier prêta ce quart de cercle à son élève, tandis que conjointement, l’abbé La Caille effectuait des relevés similaires au Cap de Bonne Espérance. L’objet de ces mesures astrométriques était de calculer la distance qui séparait la Terre de la Lune. A cette occasion, le jeune Lalande fit remarquer la précision de son travail et obtint la reconnaissance de la communauté scientifique. C’est à partir de cet épisode qu’il entama sa brillante carrière d’astronome.
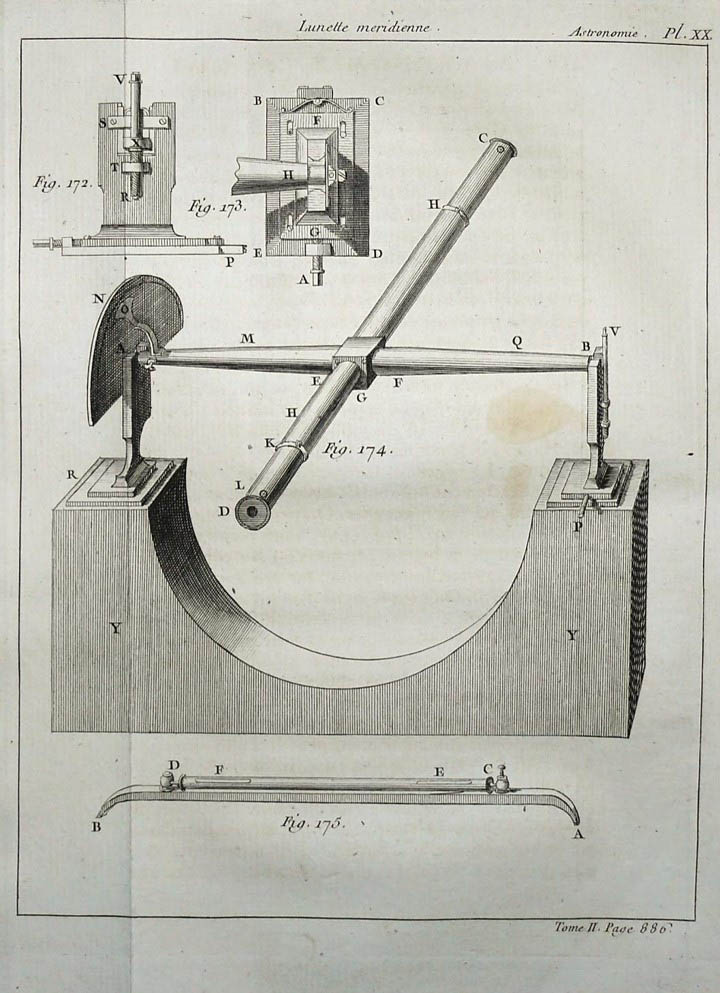
On pourrait penser que les astronomes ont toujours observé le ciel comme nous le faisons aujourd’hui avec nos instruments. Cependant, Il y a plus de deux siècles, la qualité des optiques ne permettait guère que l’observation de quelques planètes. Les galaxies se confondaient encore avec les nébuleuses à peine discernables. Les astronomes ne disposaient pas du formidable outils informatique qui est désormais capable de faire pointer automatiquement un télescope d’amateur sur des dizaines de milliers d’objets célestes en quelques secondes. Il en va de même pour disposer de l’heure exacte en tout lieu du globe, avec une précision de l’ordre de quelques picosecondes par an, alors que dans la seconde moitié du XVIIIème siècle, la précision des horloges ne dépassait pas quelques secondes par mois.
Les astronome arpentaient le ciel pour le cartographier le plus précisément possible et pour calculer les trajectoires de divers objets célestes. Cependant dans les calculs, intervenait le facteur temps, dont la détermination précise posait de gros problèmes. Les horloges mécaniques, sensibles à la température, à l’humidité ou à d’autre facteurs, ne pouvaient être parfaitement synchronisées en divers endroits du globe, sans le recours à l’astronomie. C’est la régularité de la rotation terrestre et une connaissance précise de la position des étoiles sur la sphère des fixes qui permettait alors une détermination précise du temps. La conception de la lunette méridienne permettait quant à elle de balayer un plan fixe. Si on considère parallèlement la rotation terrestre, il en résulte que ce plan va balayer, à son tour, toute la sphère céleste. Chaque fois que ce plan méridien sera en face d'une étoile donnée, il sera donc possible de déterminer l’ascension droite de cette étoile et d’en déduire le temps sidéral du lieu d’observation. Il sera ensuite possible de déterminer le temps moyen de ce lieu et de procéder au réglage des horloges. Lalande explique ainsi l’utilité de la lunette méridienne: « La nécessité où sont les astronomes d’observer sans cesse les différences d’ascension droite entre les planètes et les étoiles, les a mis dans la nécessité d’avoir des instruments qui pussent être placés bien exactement dans le méridien. Le quart de cercle mural, quelque soin qu’on prenne à le dresser exactement, ne saurait avoir un plan assez régulier et assez parfait, pour que la lunette décrive le méridien à 2’’ prés, depuis le zénith jusqu’à l’horizon; pour obtenir cette précision dans les passages au méridien, il faut recourir à une lunette montée sur un axe qui soit tourné avec grand soin; c’est ce que nous appelons lunette méridienne, ou instrument des passages. »
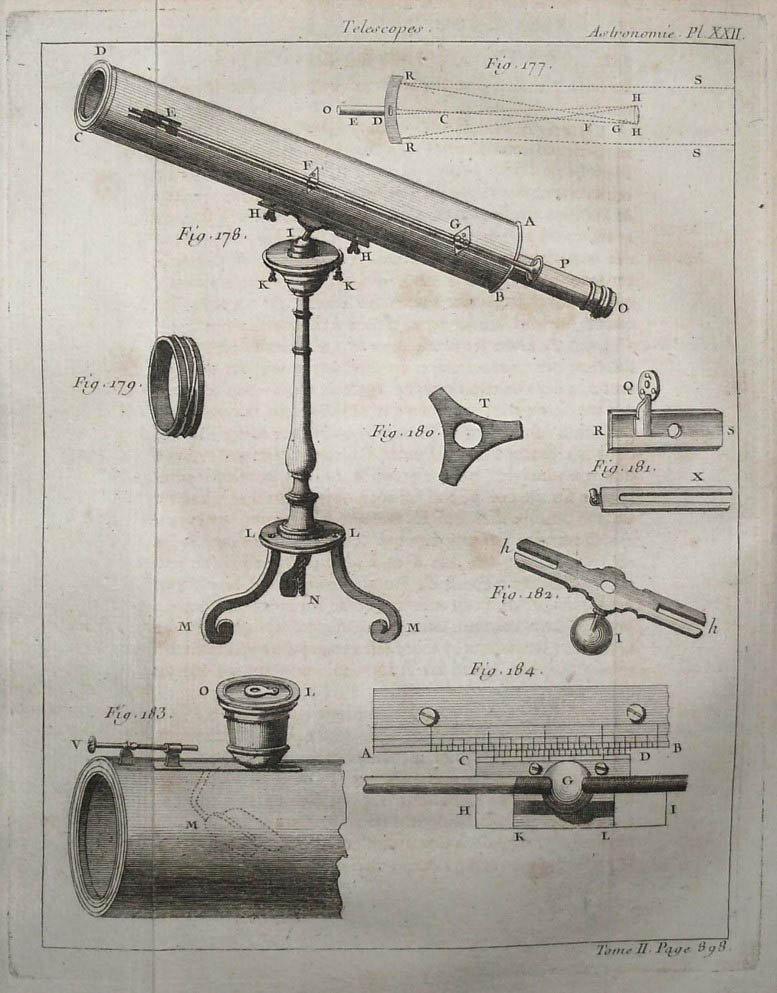
Sur la planche ci-dessus, Lalande présente un télescope « grégorien », du nom de son inventeur, l’astronome et mathématicien écossais, James Grégory (1638-1675), professeur à l’université de Saint Andrews puis à Edinburg. En 1663, ce dernier publie à Londres, "Optica promota", ouvrage dans lequel il décrit un instrument qu’il ne fut malheureusement pas en mesure de construire par manque de compétences pratiques. Le principe de ce télescope intéressa Newton qui lui apporta des perfectionnements et réalisa le télescope à réflexion portant son nom. Le télescope de Grégory eut une certaine vogue au XVIIIème siècle, mais il fut plus tard abandonné. En revanche, on retrouve des utilisations du principe de Grégory en radioastronomie, comme c’est le cas pour le dôme grégorien du télescope géant d’Arecibo.
Dans son commentaire, Lalande montre (fig.183 ci-dessus) comment un télescope grégorien peut être transformé en télescope de Newton et il conclue par une prédiction: « Il est possible d’étendre cet art beaucoup plus loin, il n’est pas encore à sa perfection, et la force des télescopes augmentera de plus en plus; si jamais la curiosité et le loisir des savants, ou la puissance des souverains vont assez loin pour faire entreprendre un télescope qui ait quelque toises de diamètre et qu’on y réussisse, nous verrons sans doute dans le ciel des choses toutes nouvelles. »