Histoire de l'Académie Royale des Sciences
De 1699 à 1740, Fontenelle fut secrétaire perpétuel de l’Académie Royale des sciences et, à ce titre, supervisa une grande part des publications de cette institution. Ainsi, durant prés de quarante ans, il veille à la rédaction de l’Histoire de l’Académie Royale des sciences dont je possède quelques exemplaires. Cette Histoire de l’Académie consiste en une présentation des articles scientifiques nommées Mémoires, qui occupent la seconde partie de ces ouvrages. Ces Articles, généralement plus dense et plus approfondis, sont rédigés ou approuvés par les membres de l’académie.
A travers ces ouvrages, Fontenelle établit les fondements de l’histoire des sciences, nouvelle discipline qui contribuera au rayonnement de la France et à la propagation du savoir scientifique à travers l’Europe entière. Voltaire, d'Alembert, Condorcet, Montucla ou Bailly perpétueront cette démarche et renforceront la prééminence du français en tant que «langue des savants». Les articles compilés dans cette œuvre couvrent la totalité des domaines scientifiques. Ainsi, pouvons-nous y lire des textes traitant de physique, anatomie, médecine, chimie, botanique, algèbre, géométrie, mécanique, géographie, acoustique, etc. et, bien sûr, d’astronomie. J’en propose ici de courts extraits, relatifs aux années 1713, 1714,1716 et 1717
Malgré le fait que les livres en ma possession proviennent d’une édition hollandaise, j’ai pu vérifier auprès de la BNF que leur contenu était identique à celui des ouvrages imprimés sur les presses royales de Paris. Seuls les privilèges y sont rédigés en hollandais et signés par Antoine Heinsius, successeur de Guillaume III, prince d’Orange et roi d’Angleterre. En mars 1713, (année restituée dans le premier volume), la paix d’Utrecht mettait un terme au conflit armé opposant la France de Louis XIV aux Pays-Bas; il n’est donc pas étonnant de trouver une telle publication provenant d’une imprimerie d’Amsterdam, si ce n’est que l’on notera en consultant la page de titre ci-dessus, que l’Histoire pour l’année 1713 ne fut éditée que six années plus tard, en 1717. C’est pourtant bien le portrait de Louis XIV (disparu en 1715) qui figure en médaillon sur la gravure du frontispice
Ce passage met l’accent sur le travail de Jacques Cassini qui, suite à des opérations de mesure du méridien terrestre, avait noté que selon la latitude où il était mesuré, un même degré d’angle donnait des distances terrestres différentes. Ces dernières diminuaient au fur et à mesure que l’on s’éloignait de l’équateur et que l’on se rapprochait du pôle. Il en déduisit que la Terre était une ellipsoïde allongée vers ses pôles. Cet extrait montre que même les savants les plus illustres peuvent faire des erreurs. Cassini, en effet, fut à l’origine d’une controverse qui dura près d’un quart de siècle et opposa ses conclusions à celles de Huygens et de Newton qui montraient par la théorie que, compte tenu de sa rotation, la Terre devait au contraire être aplatie à ses pôles. En 1737, l’expédition de Maupertuis en Laponie tranchera au détriment de Cassini.
Maraldi évoque des étoiles « changeantes » dans la constellation du Cygne. D’après sa description, la première étoile située dans la poitrine du Cygne, pourrait être P. Cygni (34 Cyg) mentionnée par Johann Bayer dans Uranométria, et dont la magnitude varie effectivement entre m3 et m6. On ne disposait pas de connaissances fiables relatives aux cycles des étoiles « changeantes » pour être en mesure d’avancer une explication satisfaisante de ce phénomène. Il faut remarquer par ailleurs que, selon les cas étudiés, des variations importantes de magnitude pouvaient rendre l’étoile invisible à l’œil nu et, de ce fait, donner l’impression de voir apparaitre une nouvelle étoile lorsque la luminosité de cette même étoile ré-augmentait pour la rendre de nouveau perceptible à l’œil. La qualité médiocre des instruments de l’époque, ainsi que le caractère progressif des variations de luminosité de telles étoiles, posaient également de réels problèmes en ce qui concerne l’évaluation d’une éventuelle périodicité.
En ce début de XVIIIème siècle, les étoiles variables sont un sujet d’étude à part entière. Maraldi émet ici l’hypothèse que les variations de luminosité peuvent avoir des causes similaires à celle constatées par Cassini sur des satellites de Jupiter ou de Saturne. Il fait allusion à l’hypothèse de Giovanni Baptista Riccioli qui, vers 1650, avait étudié Mizar (étoile de la Grande Ourse) pour découvrir qu’il s’agissait d’une étoile double. Cette hypothèse pertinente supposant la présence d’étoiles orbitant l’une autour de l’autre allait ouvrir une voie qui trouvera son prolongement quelque siècles plus tard et permettra d’aboutir à la découverte des premières exo-planètes
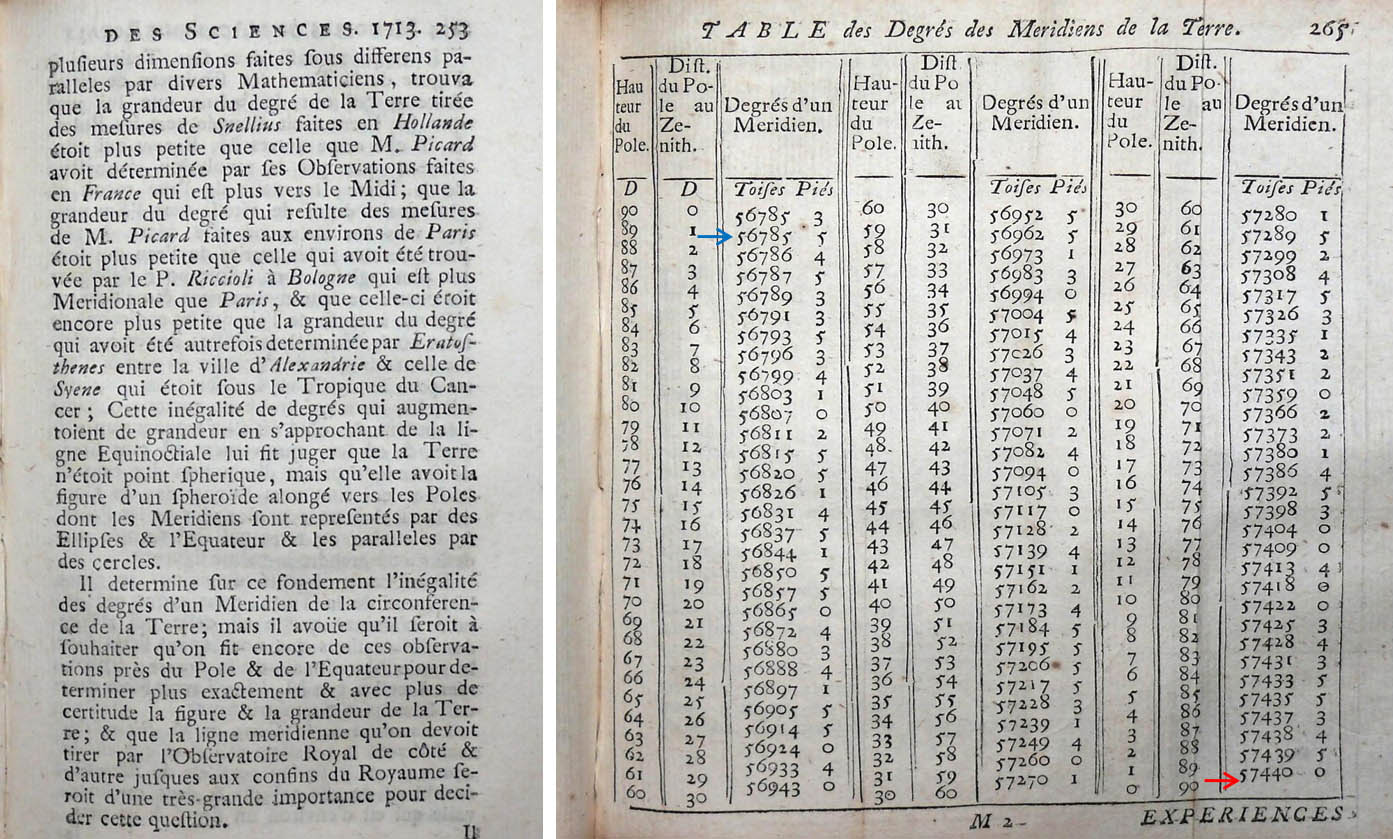
A propos de «la figure» (la forme) de la Terre, Cassini évoque succinctement les anciens, avant de traiter de questions non résolues en son temps et, plus particulièrement, des positions défendues par Newton et Huygens à ce sujet. Réfutant les hypothèse de ces derniers, quand aux écarts de longueur du pendule, il présente un point de vue inverse, soutenu par un certain Johann Caspar Einsenschmidt (1656-1712) mathématicien associé de l'Académie des sciences. Ce dernier s’appuyait sur des données relevées par Snellius, Picard ou Riccioli, pour déduire que la Terre n’était pas aplatie, mais bien allongée à ses pôles à la manière d’un fuseau. Comme je l’ai déjà évoqué, Cassini se rangera dans un premier temps à cet avis. Je montre, page suivante, un tableau des degrés des méridiens de la Terre qui l’ont, des années durant, conforté dans cette voie.
Pour mesurer le méridien, Picard et Cassini utilisèrent la triangulation dès 1670 entre Dunkerque, l’Observatoire de Paris et Collioure. L’écart entre ces deux derniers points étant établi à 6°18’57’’, Cassini put extrapoler pour produire ce tableau. Ce dernier fait apparaitre qu’un degré de méridien au pôle nord (flèche bleue) est évalué à 56.785 toises, alors qu’à l’équateur (flèche rouge), il est évalué à 57.440 toises. Cassini écrit: « Il résulte que les degrés qui sont vers le Septentrion sont plus petits que ceux qui sont vers le Midi, et que par conséquent la figure d’un méridien de la Terre doit être telle que les degrés augmentent plus on s’approche de l’équateur et diminuent au contraire en allant vers les pôles…». À partir de là, il lui devint aisé de montrer que la Terre était une ellipse dont le grand axe est celui des pôles et le petit axe, celui de l’équateur. Malheureusement, ses mesures de référence étaient erronées.
L’observation de la grande tache de Jupiter permit à Cassini, dés 1665, d’établir la durée de la révolution de cette planète. Cet article relate un travail qu’effectua Maraldi sur cette même tache ainsi que sur les bandes «passagères» qui apparaissent à la surface de Jupiter. C’est à l’occasion d’une réapparition de la tache, en 1708, que Maraldi décide d’effectuer une nouvelle fois la mesure de la rotation cette planète. On ne manquera pas de noter les divers paramètres dont devaient tenir compte les astronomes lors de telles expériences. En effet, il ne s’agissait pas simplement de compter le temps écoulé entre deux apparitions de la tache en un même lieu du disque visible de Jupiter, mais bien d’y inclure d’autres paramètres comme, par exemple, les écarts de mesures dus aux changements de position de l’observateur (situé lui aussi sur un astre en mouvement, en l’occurrence la Terre). L’exemple donné ici, à ce propos, qui s’appuie sur une analogie avec la rotation du Soleil, est on ne peut plus explicite.
La situation de l’observateur n’était pas le seul paramètre à prendre en considération. En effet, on remarque ici que le mouvement de la tache paraissait plus rapide, dès lors qu’elle se situait plus près du «milieu» du disque. Ce qui se comprend dans la mesure où le disque qui apparait visuellement à l’observateur, est en réalité une surface sphérique. La tache, elle-même, subit des déformations apparentes selon sa position: circulaire au milieu du disque, elle devient elliptique au fur et à mesure où elle se rapproche des bords du disque. En dépit de toutes ces difficultés, Maraldi confirme les mesures de Cassini. Si l’on considère son résultat : 9h 56’ 49’’ comparé aux mesures actuelles les plus précises, soit: 9h 55’ 27,3’’, l’erreur de Maraldi est à peine supérieure à 1 seconde, soit l’équivalent de 0.003% !
En 1714, l’adhésion des académiciens aux théories cartésiennes laisse peu d’espace au développement d’autres théories. De l’avis de ces illustres savants, Saturne appartiendrait au «tourbillon du Soleil». Ce extrait supposant une bonne connaissance des «sections coniques» explique ce que verrait un observateur situé sur le Soleil, s’il regardait en direction de la Terre. Selon les positions successives de notre planète au cours des saisons, la ligne imaginaire matérialisant les lieux du centre de la zone visible (éclairée) de la Terre, lui apparaitrait comme une droite, s’il était situé dans le plan du ½ cercle qu’elle définie (cas de l’équateur), alors que s’il se trouvait hors de ce plan, cette même ligne prendrait l’aspect d’une ellipse dont l’ouverture dépendrait de la position de cet observateur, relativement au plan du ½ cercle évoqué précédemment (cas des tropiques).
Les observations de Cassini permettent de comprendre comment l’inclinaison de l’axe de rotation de Saturne (26.73°) fait varier l’aspect de ses anneaux. Ainsi, tous les 14,5 ans environ (moitié d’une révolution de saturne, soit: 29 ans 165 j et 11,68 h), ces derniers se présentent à nous alternativement de face puis sur leur tranche, dont la faible épaisseur ( à peine quelques mètres ) les rend invisibles pour un observateur lointain.
NB: Depuis que l’on connait la constitution des anneaux on a également pu expliquer leurs écarts de luminosité: lorsque le Soleil se trouve aligné avec la Terre et Saturne, ces anneaux ont un éclat maximal car, pour l’observateur situé sur la Terre, chaque particule éclairée qui les constitue cache alors sa propre ombre. Inversement, dans les autres cas, la brillance est moindre car ces mêmes particules projettent leurs ombres les unes sur les autres.
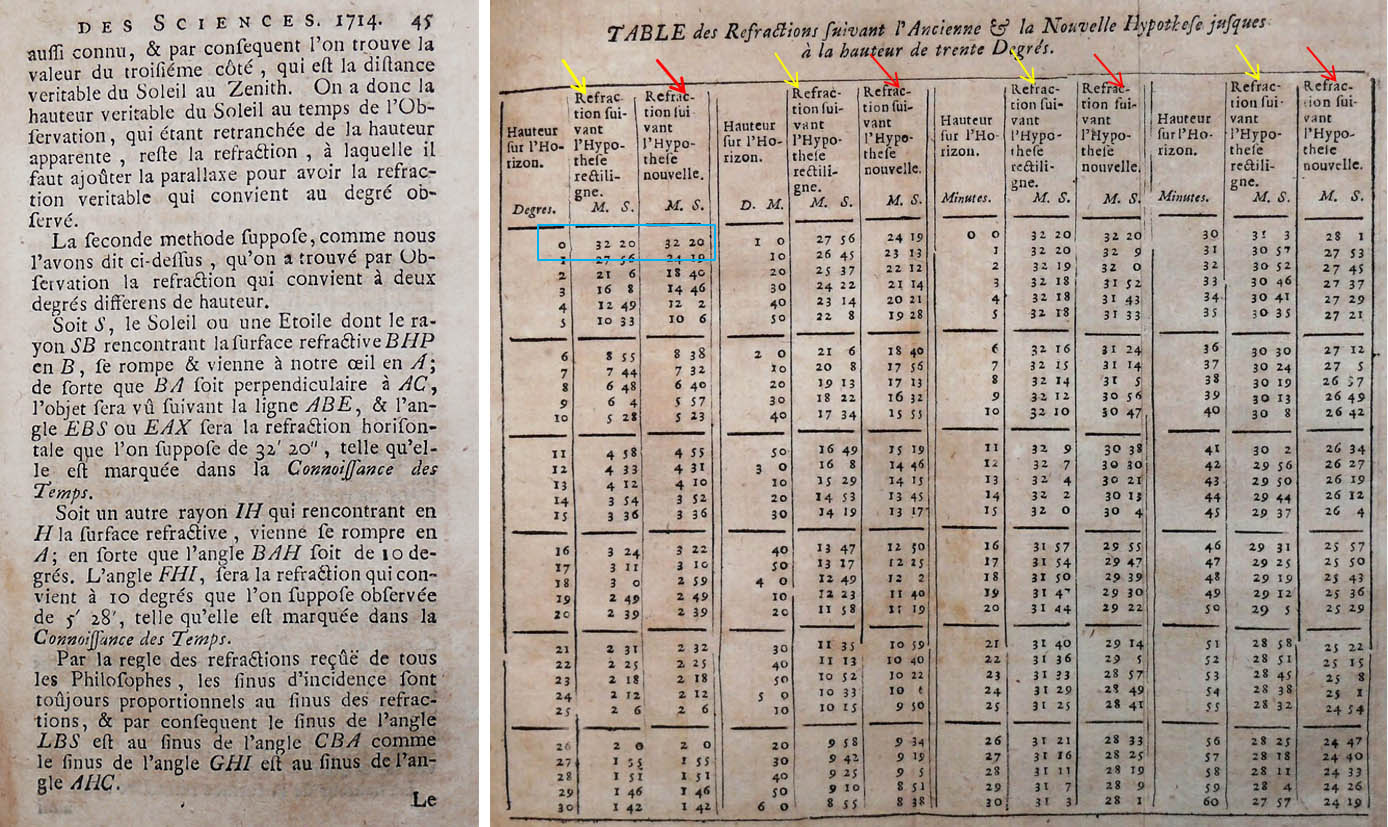
Les «réfractions astronomiques», correspondent à la réfraction atmosphérique qui «déplace les astres» en donnant à l’observateur l’illusion que ces derniers occupent des positions différentes de leurs positions réelles dans le ciel. Cette réfraction impose des correctifs dès lors qu’il s’agit de mesurer précisément la position d’un objet céleste. Pour l’évaluer, on se basait sur les observations d’un même objet effectuées en des points distants. La méthode convenait pour les objets situés non loin de la ligne d’horizon où un degré représente, pour un rayon lumineux, un différentiel bien plus important de distance à travers l’atmosphère que si ce même degré avait été situé sur une ligne dont la direction se rapprocherait de la verticale. Pour cette évaluation, on utilisait le Soleil dont on comparait la position observée (relative) avec la position réelle déterminée à partir de son mouvement (15°/h = 360°/j). Le tableau de la page suivante est donc établi depuis l’horizon jusqu’à 30° de hauteur.
Dans les pages qui suivent cet extrait, Cassini développe le détail des calculs lui permettant d’établir les incidences de la réfraction. Il établit ce tableau en y intégrant les résultats selon deux modes de calcul distincts. L’hypothèse dite «rectiligne» (flèche jaune) prend en compte le cas où les rayons lumineux ont une trajectoire rectiligne durant leur parcours à travers l’atmosphère. Les mesures effectuées par Cassini lui font cependant envisager que la trajectoire de ces rayons lumineux puisse être parabolique ou qu’elle décrive des arcs de cercle; il en déduit une Hypothèse nouvelle» (flèches rouges). On notera que le degré « 0 » correspond à une valeur de réfraction dite «horizontale» de 32’ 30’’, alors admise par tous les grands astronomes. A juste titre, Cassini montre ici sa préférence pour l’hypothèse des trajectoires curvilignes, tout en soulignant également l’impact de l’humidité «vapeurs» et de la température de l’air. Selon les saisons, il préconise l’usage de tables correctives appropriées.
On se souviendra de l’intérêt particulier que portait Louis XIV à l’Académie des sciences. Son attention trouva un prolongement à travers celle que lui porta également le duc D’Orléans, régent du royaume jusqu’à la majorité de Louis XV. L’extrait ci-dessus montre qu’il fit évoluer le règlement de cette institution royale. En date du 3 janvier 1716 et au nom du futur roi, il y apporte des compléments concernant les associés et les adjoints. En prenant effectivement la tête de l’Etat en 1726, Louis XV continue l’œuvre entreprise par son arrière grand-père et promeut activement la diffusion des connaissances scientifiques. Lui-même avait étudié la géographie, l’astronomie et les mathématiques et était considéré comme un prince savant. Ainsi, lors de l’éclipse du 19 décembre 1722, ordonna-t-il à Jacques Philippe Maraldi et à Jean Dominique Cassini d’effectuer une observation depuis Versailles, à laquelle il assista en personne depuis « un salon situé à l’extrémité de la grande galerie, et qui regarde le sud-ouest ».
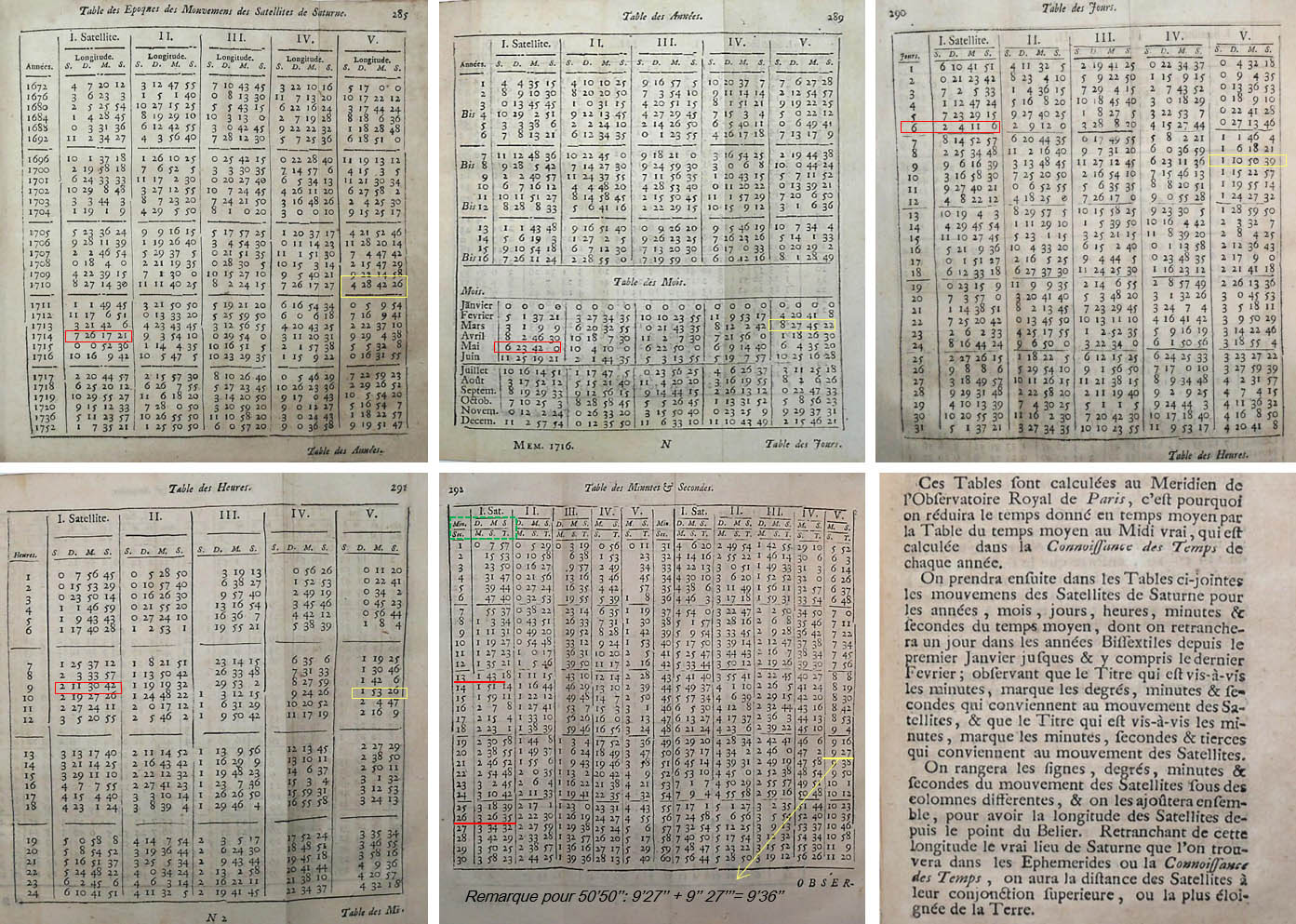
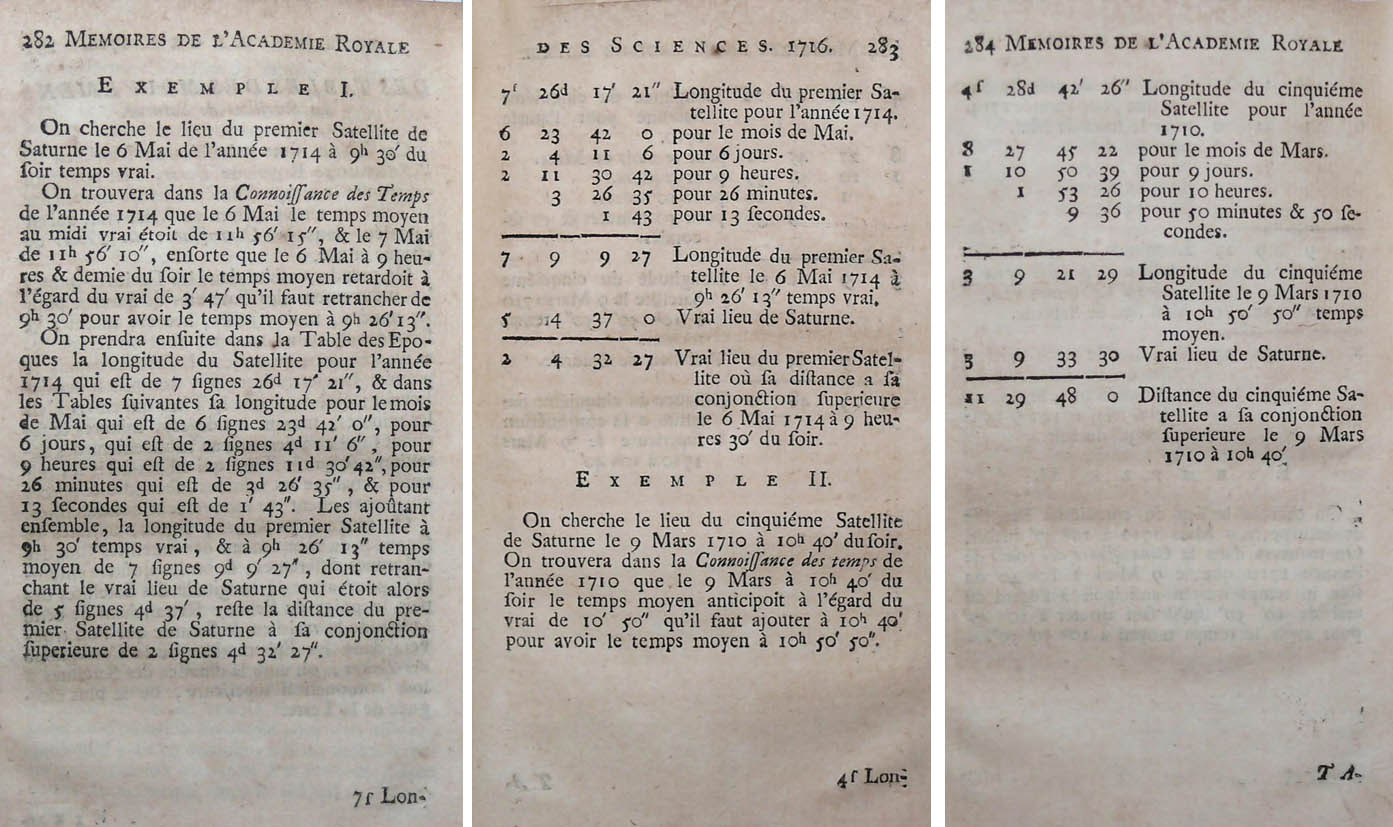
A travers les deux exemples traités ci-dessus, je propose de suivre la démarche d’un astronome du début du XVIIIème siècle qui aurait voulu connaitre la position d’un satellite de Saturne pour un jour et une heure donnés (la manière de procéder était la même pour les satellites de Jupiter). Pour cela, j’ai reproduit (page du dessus) les tableaux nécessaires à l’établissement des lieux de ces objets. Les valeurs relatives au premier exemple sont encadrées en rouge et celles relatives au second exemple sont encadrées en jaune. Les commentaires montrent également l’importance de ramener les heures courantes aux heures pour lesquelles sont établies les tables des mouvements. Lorsqu’on sait que ces calculs étaient fais à la main, on mesure la masse de travail nécessaire et on ne peut que se féliciter que nos logiciels actuels réalisent ce type d’opérations en quelques infimes fractions de secondes.
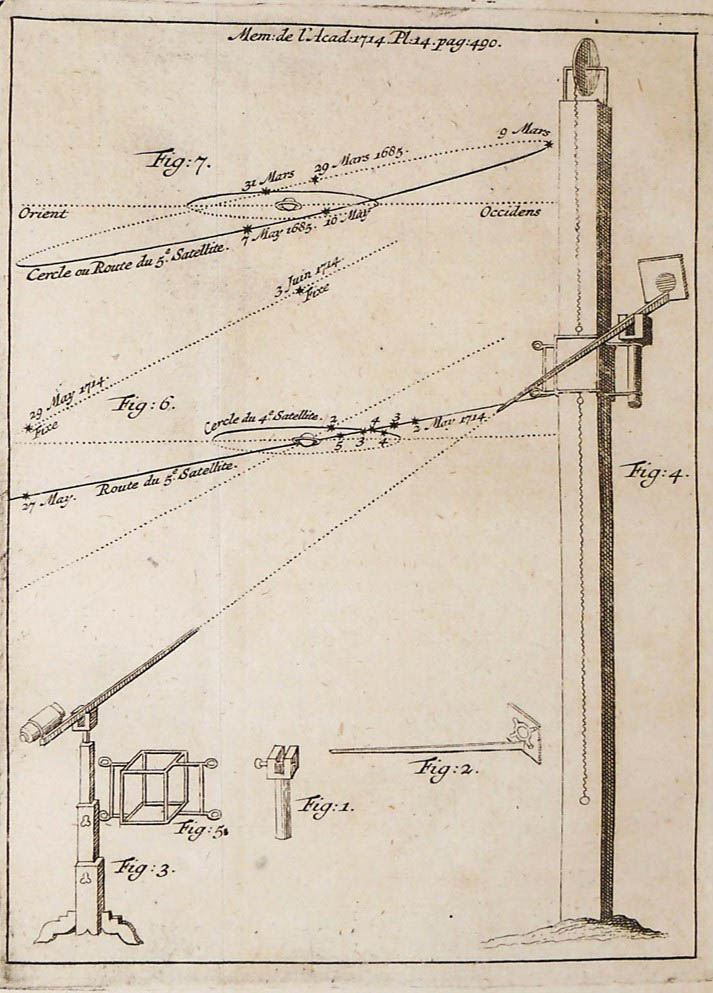
Cette planche contient deux figures montrant les positions orbitales du cinquième satellite de Saturne pour les mois de mars et mai 1685 (fig.7) et pour mai 1714 (fig.6). L’observation de ce satellite découvert en 1671 par J.D Cassini (Ier) posait des problèmes aux astronomes, car elle nécessitait l’utilisation de lunettes à très longs foyers (distance focale). Ainsi, Cassini utilisa une lunette de trente quatre pieds de long (environ onze mètres de longueur), dont je reproduis ci-dessous une gravure. On mesure à quel point il devait être fastidieux de manipuler ces lourdes et encombrantes lunettes. Huygens avait cependant conçu une lunette aérienne moins encombrante plus maniable et sensée être facile à mettre en œuvre rapidement et en tout lieu.
La petite image ci-contre montre l’usage de cet instrument dont l’objectif et l’oculaire n’étaient reliés que par un fil tendu permettant l’alignement des parties optiques. J.D Cassini exploita cette lunette « aérienne ». Son fils Jacques commente : «Ce fut dans ce dessin que mon père essaya de se servir de Lunettes sans tuyau, plaçant le Verre Objectif sur le haut de la terrasse de l’Observatoire, & tenant l’Oculaire à la main à la distance du foyer dans la direction de l’Astre & de ces deux verres… On ne pouvait observer Saturne par ce moyen que dans certaines heures, principalement à son passage au méridien… Pour remédier à cet inconvénient on fit transporter de Marly une tour de bois de 20 toises de haut…on employa pour porter le verre une machine armillaire composée de Cercles de la sphère, avec un mouvement à ressort, semblable à celui d’une horloge… Ces méthodes eurent le succès que l’on en attendait & nous avons un grand nombre d’observations qui y ont été faites pendant plusieurs années …» La version originale de ce télescope fut améliorée, ce qui permit à Jacques Cassini de conclure: « l’objectif… se dirige très exactement à l’Astre par le moyen d’une corde tendue & attachée à la queue des deux supports… cela s’exécute avec tant de promptitude & de facilité, qu’on peut assurer qu’il n’y a guères de méthodes plus simple dans la construction, & en même temps plus commode dans la pratique: deux avantages très importants pour le progrès de l’Astronomie ».
En 1717, on mesure les distances entre la Terre et les planètes en utilisant la parallaxe «horizontale» ou «annuelle». Pour les étoiles, la mesure de la parallaxe «horizontale» est inexploitable. En effet, au delà de Mars, les valeurs angulaires mesurées sont trop insignifiantes. Les astronomes imaginent alors établir le rapport des grandeurs entre une étoile et le Soleil pour en déduire l’éloignement de cette étoile. Ils s’appuient sur la distance* entre la Terre et le Soleil, alors évaluée à trente trois millions de lieues, (128.634.000 km, en 1713. Une lieue = 3,898 km). Seulement, pour que cette mesure soit valide est-il encore indispensable que la taille de l’étoile soit identique à celle du Soleil, hypothèse absolument invérifiable.
* Cette «distance» est en réalité égale au demi-grand axe de l’orbite de la Terre autour du Soleil aujourd’hui connue sous le nom d’unité astronomique «ua». 1ua = 149 597 870 km,. On pourra noter que l’erreur entre la valeur réelle et celle estimée au début du XVIIIème siècle est de l’ordre de 16%.
Une telle mesure restait donc, pour l’instant, très aléatoire et même les plus illustres astronomes se heurtaient à cet écueil. Les angles de parallaxe sont trop insignifiants pour être exploités, en dépit des précautions prises. Il faut remarquer que ces difficultés rencontrées par les astronomes eurent pour effet positif d’induire l’amélioration qualitative de l’instrumentation ainsi que celle des procédures de mesure. Lorsque Cassini évalue la distance de Sirius, il obtient des valeurs angulaires infimes, de l’ordre de quelques secondes, équivalentes à celles que pourrait causer la réfraction atmosphérique. Il parvient cependant à établir que Sirius devrait se trouver à une distance 43.700 fois plus éloigné de la Terre que ne l’est le Soleil (ce qui, selon mon évaluation, revient à un éloignement d’environ 0,9 al). Cette mesure, fort éloignée de la valeur réelle (Sirius est situé à 8,6 al), permit cependant de révéler aux astronomes des ordres de grandeur absolument « prodigieux », en ce qui concerne les distances en jeu dans l’Univers.
Dans l’extrait ci-dessus et en page suivante, on peut comparer les compte-rendus d’observations d’une éclipse de Lune, effectuées respectivement par Philippe de la Hire et par Jacques Cassini. Les éclipses faisaient partie des phénomènes les plus observés, en tant que moyen d’affiner la connaissance des trajectoires des planètes et de leurs satellites; elles permettaient la vérification des calculs théoriques et des équations de la mécanique céleste. Outre les relevés qui mettent en relation la position de l’ombre avec l’heure de son passage, et qui serviront aux calculs ultérieurs, on peut remarquer que les commentaires mettent en évidence les difficultés liées aux conditions météorologiques rencontrées lors de ces évènements.
On constate, en premier lieu, les écarts entre les relevés des deux astronomes effectués pourtant tous deux depuis l’Observatoire Royal de Paris, ce qui permet d’écarter toute hypothèse de décalage concernant l’heure de référence. Les valeurs de ces écarts de 1’ 50’’ pour le début de l’éclipse, de 3’ pour une Lune éclipsée de «5 doigts et de 15’’» pour la fin de l’éclipse peuvent donc paraitre importantes. Pour avoir moi-même eu l’occasion d’observer avec attention une éclipse de Lune en avril 2007, j’ai, pu vérifier que les bords de la zone d’ombre que la terre dessine sur la surface lunaire sont assez flous et que leur limite est très délicate à déterminer. Indépendamment donc de l’instrument utilisé et selon les individus l’acuité visuelle peut porter à des interprétations sensiblement différentes, ce qui permet de justifier les écarts d’appréciation entre ces deux astronomes, par ailleurs observateurs aguerris.
Ce passage est celui auquel renvoient les commentaires de l’Histoire de l’Académie, dont j’ai donné un extrait (deux commentaires plus haut). Je reproduis ici l’intégralité des mémoires de Jacques Cassini concernant la mesure de l’éloignement des étoiles par la méthode de la parallaxe annuelle. Cassini II note que le mouvement apparent « presque insensible » des étoiles fixes, résulte d’une variation du mouvement propre de notre planète. Selon lui, la méconnaissance des valeurs exactes de ce mouvement et le manque de précision des instrument suffiraient à fausser les mesures de parallaxe. Constatant le peu de fiabilité des conclusions que tirent certains de ses collègues, Cassini s’apprête à effectuer ses propres observations avec la plus grande rigueur qui se puisse, compte tenu des moyens de son temps (voir la suite).
Cassini II compare, dans un premier temps, les diamètres apparents de Sirius et de Jupiter. Afin que ses mesures soient effectuées dans des conditions identiques, pour minimiser les dispersions propres à l’utilisation d’instruments différents, il use d’une même lunette. En premier lieu, il constate que le diamètre apparent de Jupiter est dix fois plus grand que celui de Sirius. Il peut alors exploiter une règle simple de trigonométrie qui lui permet de déduire que le diamètre de l’étoile est de deux fois et 1/3 plus grand que celui de la Terre. Mais ce résultat n’est valable que dans la mesure où il suppose une distance de Sirius à la Terre équivalente à celle de Saturne. Cassini va donc émettre une nouvelle hypothèse, en se basant sur l’avis des « philosophes », qui consiste à considérer que les étoiles fixes sont « autant de Soleils » et qu’elles doivent en conséquence présenter des grandeurs comparables. Dans ce cas, les mesures qu’il a effectuées lui permettent de déterminer, non plus la grandeur de l’étoile, mais son éloignement. Les résultats prennent alors de toutes autres proportions…
Cassini souhaite mesurer la parallaxe annuelle des étoiles. En effet, la distance qui sépare les positions respectives de notre planète autour du Soleil à six mois d’intervalle, pourrait permettre la mise en évidence d’une différence angulaire de positionnement pour une étoile donnée sur cette période. Cet écart angulaire fournirait un autre moyen que la comparaison des diamètres pour calculer la distance des étoiles. Cassini fait alors référence à Picard et à ses relevés sur l’étoile polaire, qui ont mis en évidence ce type d’écarts angulaires. On remarquera que Cassini évoque également l’incidence possible de la précession des équinoxes sur ces mesures. Il décide cependant de réitérer l’expérience avec Sirius, notamment en raison de le luminosité de cette étoile, de sa position dans le ciel proche de l’horizon et de sa taille qui laisse supposer qu’elle est plus proche de nous que d’autres étoiles de moindre grandeur apparente.
L’auteur donne encore quelques raisons qui l’ont conduit à opter pour la mesure de la distance de Sirius, en particulier sa faible variation de déclinaison qui lui fait «longer» l’écliptique tout au long d’une année et qui, de ce fait, permet une meilleure discrimination de l’incidence de ses variations. La manipulation consiste à positionner une lunette, de telle sorte que Sirius apparaisse dans un réticule constitué de deux paires de fils formant un carré et qui permettra de visualiser tous ses changements de position. La lunette est solidement fixée, de sorte qu’aucun évènement extérieur ne puisse modifier sa position durant la période des mesure, qui s’étalera d’avril 1714 à juin 1715. Cassini détaille ensuite les observations réalisées et prend toutes les précautions, relativement à leur interprétation.
Pour attester de la fiabilité de ses mesures, Cassini montre comment il a pu s’assurer que sa lunette n’avait pas bougé depuis son positionnement initial. Il explique ensuite le raisonnement qui lui permet de conclure que l’incidence de la réfraction atmosphérique ne pouvait non seulement amplifier les écarts de position de l’étoile dans le réticule mais, bien au contraire, qu’elle ne pouvait que s’y opposer. Ce qui avait pour effet de rendre les mesures encore plus significatives, au risque même d’avoir pu en minimiser les valeurs. Dès lors, Cassini peut calculer la distance de Sirius à la Terre à partir d’une parallaxe estimée à 6 ’’. En réalité la parallaxe de Sirius, mesurée avec les instruments modernes les plus précis dont disposent les astronomes est de 0,371’’. Nous verrons, page suivante le résultat auquel parvient Cassini, ainsi que le commentaire qu’en fit Jérôme de la Lande quarante sept ans plus tard.
Les deux pages ci-dessus à gauche, sont extraites de l’Astronomie de Lalande, publié en 1764, dont je présenterai quelques extraits dans un article. Depuis l’expérience de Cassini, les connaissances en astronomie avaient considérablement évolué, notamment grâce à la découverte par James Bradley de l’aberration des étoiles.
Lalande a pris soin de vérifier les travaux effectués par Picard à Uraniborg et mentionnés par Cassini, pour en déduire qu’ils étaient « fort conformes », compte-tenu de la découverte ultérieure de Bradley. N’enlevant rien au mérite de ses prédécesseurs qui jouèrent les pionniers en la matière, Lalande conviendra que la parallaxe relevée par ces derniers pouvait avoir de multiples causes. Il s’exprimera en ces termes: «On doit considérer six espèces de mouvements dans les étoiles fixes, la précession, l’aberration, la nutation, le changement général de latitude, les changements particuliers à différentes étoiles, et la parallaxe annuelle…». Ce qui explique qu’une part d’entre elles n’ont pu être prises en considération par Cassini. Lalande, en accord avec les astronomes de son temps conclut: «La parallaxe annuelle est absolument insensible et comme nulle dans les étoiles fixes».