Abbé La Caille - Leçon d'astronomie

Nicolas-Louis de La Caille , fut l’une des principale figure de l’astronomie d’observation du XVIII^ème siècle. Le livre, dont je donne ici quelques extraits, est la quatrième édition, augmentée par De La Lande et publiée en 1780, de son premier ouvrage paru en 1749 (La Caille est mort en 1762). L’essentiel du contenu se compose d’un exposé d’astronomie géométrique, accompagné des démonstrations qui s’y rattachent. A la différence des ouvrages présentés dans le volume précédent, celui-ci peut paraitre plus difficile à lire si l’on considère qu’il ne comporte que très peu de digressions, tant au niveau des commentaires historiques que des réflexions personnelles de l’auteur. Jérôme de Lalande y fait d’ailleurs référence dans la préface (voir ci-dessous), lorsqu’il avance que tel fut le souhait de l’auteur. La Caille aborde donc l’astronomie sous l’angle du géomètre ou du physicien, ce qui n’empêchera nullement le présent ouvrage de connaître un important succès en France et à l’étranger, puisqu’il fut traduit en latin, grec, Italien et portugais. Il fit également l’objet de nombreuses rééditions, jusque dans le premier quart du XIX^ème siècle. La carrière d’astronome de La Caille fut brève, comparée à celles de ses contemporains comme Clairaut, Messier, Maupertuis ou De La Lande. Il la commence en effet vers l’âge de vingt sept ans, en cartographiant la côte atlantique et en corrigeant sensiblement les erreurs de ses prédécesseurs. De retour à Paris, le jour, il enseignait les mathématiques au collège Mazarin tandis que la nuit, il traçait des cartes du ciel parisien. Il établit une liste de toutes les éclipses à venir pour une durée de cinquante ans et fit preuve, à cette occasion, d’une rapidité de calcul que Diderot qualifia de « sidérante ». Son souhait le plus vif de cartographier le ciel austral, se réalisa en 1751, lorsqu’il se rendit en Afrique du Sud. A cette occasion, il découvrit et classifia plus de dix mille étoiles et il inventa quatorze nouvelles constellations, en utilisant une lunette de seulement 32 pouce (env.80 cm). On peut lire, à ce sujet, dans l’éloge de La Caille par Jean Sylvain Bailly, publié en 1770: « On s’étonnera peut-être qu’il n’ait pas employé pour ses observations une lunette plus longue que trente deux pouces, mais ce choix même était une preuve de son habileté: le vent de sud-est qui règne une bonne partie de l’année au Cap de Bonne-espérance, occasionne aux astres un sautillements et une fausse augmentation de diamètre qui nuit beaucoup à déterminer leur position, et que M. l’abbé de la Caille n’avait pu diminuer qu’en employant une lunette plus courte que celle qu’on emploie ordinairement ».

Dans cette préface de « l’éditeur », signée en réalité par Jérôme de Lalande, ce dernier n’hésite pas à qualifier cet ouvrage de: « bien succin ». Si l’on considère le volume de son propre traité d’Astronomie, on peut effectivement comprendre sa remarque. On constatera par ailleurs, à propos de Lalande, que ce dernier manque rarement une occasion de faire de la publicité pour ses propres ouvrages, en l'occurrence son traité d’Astronomie. Attitude cavalière et en tout cas peu scrupuleuse, notamment si l’on considère qu’il utilise quand même une introduction au travail d’un confrère en tant que levier de promotion pour ses propres écrits.

L’avertissement de La Caille est sans équivoque: les splendeurs du ciel son l’œuvre de Dieu. Concernant l’astronomie, il perçoit clairement le tournant que négocie, sous ses propres yeux, cette science qu’il évoque. Il précise à propos de son ouvrage, qu’il n’est qu’un extrait de ce que d’autres grands géomètres ont écrit sur le sujet. Il conclura quelques ligne plus loin : « A la réserve de l’explication physique des mouvements de la Lune, dont le fond est en partie de s’Gravesande, tout le reste n’est autre chose que ce que j’ai pu mettre à la portée de ceux qui entendent les éléments de Mathématiques que j’enseigne; je ne l’ai rédigé que sur les connaissances que j’ai acquises, tant par mes réflexions que par mes observations, depuis vingt cinq ans que je fais de mon unique occupation de l’Astronomie ».

On remarque encore dans la note de l’éditeur, que Lalande juge qu’entamer ainsi un exposé d’astronomie, par le biais de la trigonométrie, est propre à « rebuter ceux qui commencent ». La Caille sait tout aussi bien que Lalande que l’astronomie est fondées sur la mesure des angles, il aborde en effet les premières pages de son ouvrage par une revue de formules trigonométriques dont il considère la maitrise comme un préalable incontournable. Au XVIII^ème siècle, l’astronome ne peut faire l’économie d’une solide formation en mathématique et en géométrie. L’astronome amateur, tel qu’on le connaît de nos jours n’a heureusement nul besoin de maitriser ces fondamentaux, l’informatique et les considérables progrès de l’optique s’y substituent, pour lui permettre de se livrer à une forme bien plus contemplative de l’astronomie, à laquelle les grands astronomes des siècles passés n’auraient certainement pas pu avoir accès.

La trigonométrie sphérique comprend un ensemble de relations comparable à celles de la trigonométrie euclidienne, à la différence qu’elle traite des angles et des distances repérables sur une sphère (et non plus dans un plan). Par exemple, elle permet de résoudre la somme supérieure à 180° des angles d'un triangle situé sur une sphère, à la surface de laquelle les segments de droites deviennent des arcs de cercles. En astronomie, la trigonométrie sphérique permet des calculs relatifs au système de coordonnées angulaires: déclinaison, ascension droite, angle horaire, azimut et distance zénithale. L’aspect rébarbatif de ces leçons de La Caille est ainsi commenté par un de ses contemporains, Aimé Henri Paulian (1722-1802) professeur de physique: « Ce n’est, je l’avoue, qu’à la troisième ou quatrième lecture qu’on en comprend toute la beauté; mais le plaisir délicat qu’occasionne la découverte des vérités qu’il contient, dédommage bien abondamment le lecteur de la peine qu’il a eu à trouver les opérations dont M. l’Abbé La Caille n’a donné pour l’ordinaire que le résultat. C’est là le rude et pénible travail auquel doivent courageusement se condamner tous ceux qui veulent étudier plus que superficiellement le Traité... »

Une des particularité de cette « Première section », tient au fait qu’y apparait un observateur que l’auteur situe sur le Soleil; position peu commune, mais utile pour se représenter les mouvements célestes. La Caille qui a étudié les mouvements apparents du Soleil (observés depuis la Terre), a relevé quelques irrégularités, qu’il impute à l’attraction gravitationnelle de la Lune sur notre planète. Entre 1751 et 1753, alors qu’il est au Cap, il affine ses observations et établit de nouvelles tables solaires, tandis qu’au même moment, Clairaut, d’Alembert et Euler développent les bases analytiques de cette théorie, prenant en compte les perturbations subies par la Terre de la part de la Lune, de Jupiter et de Vénus. Les tabulae solare de La Caille auront une importance historique, dans la mesure où elles seront les premières à contenir les irrégularités dues à l’aberration stellaire et à la nutation, découvertes par Bradley, ainsi que l’influence gravitationnelle de notre satellite et des planètes.

La Caille dresse ici un inventaire des objets dont il étudie les mouvements. Outre leurs trajectoires, il évoque l’existence d’autres mouvements de ces corps, mis en évidence par les variations de positions des taches visibles à leur surface. Dans cet extrait, on notera le commentaire de Lalande qui, évoque la possibilité que ces taches, visibles sur certains astres, pourraient indiquer que ces derniers soient habités. La Caille, quand à lui, n’en fait pas état et se contente d’analyser la mécanique de ces objets, dont il donne ultérieurement trois axiomes.
1) « Les effets sont proportionnels à leurs causes  ».
2) « Un corps n’a de lui-même aucune vertu, aucune force pour changer son état de repos ou de mouvement ».
3) « Une puissance motrice qui fait un effort sur un corps, soit en repos, soit en mouvement, y éprouve une résistance proportionnelle à la masse de ce corps et à la vitesse que la puissance tend à lui donner. Cette résistance détruit une partie de la force de la puissance motrice, et elle fait le même effet que si le corps résistant était animé d’une force égale à la force détruite, et dirigé en un sens opposé à celui dans lequel elle agissait. »

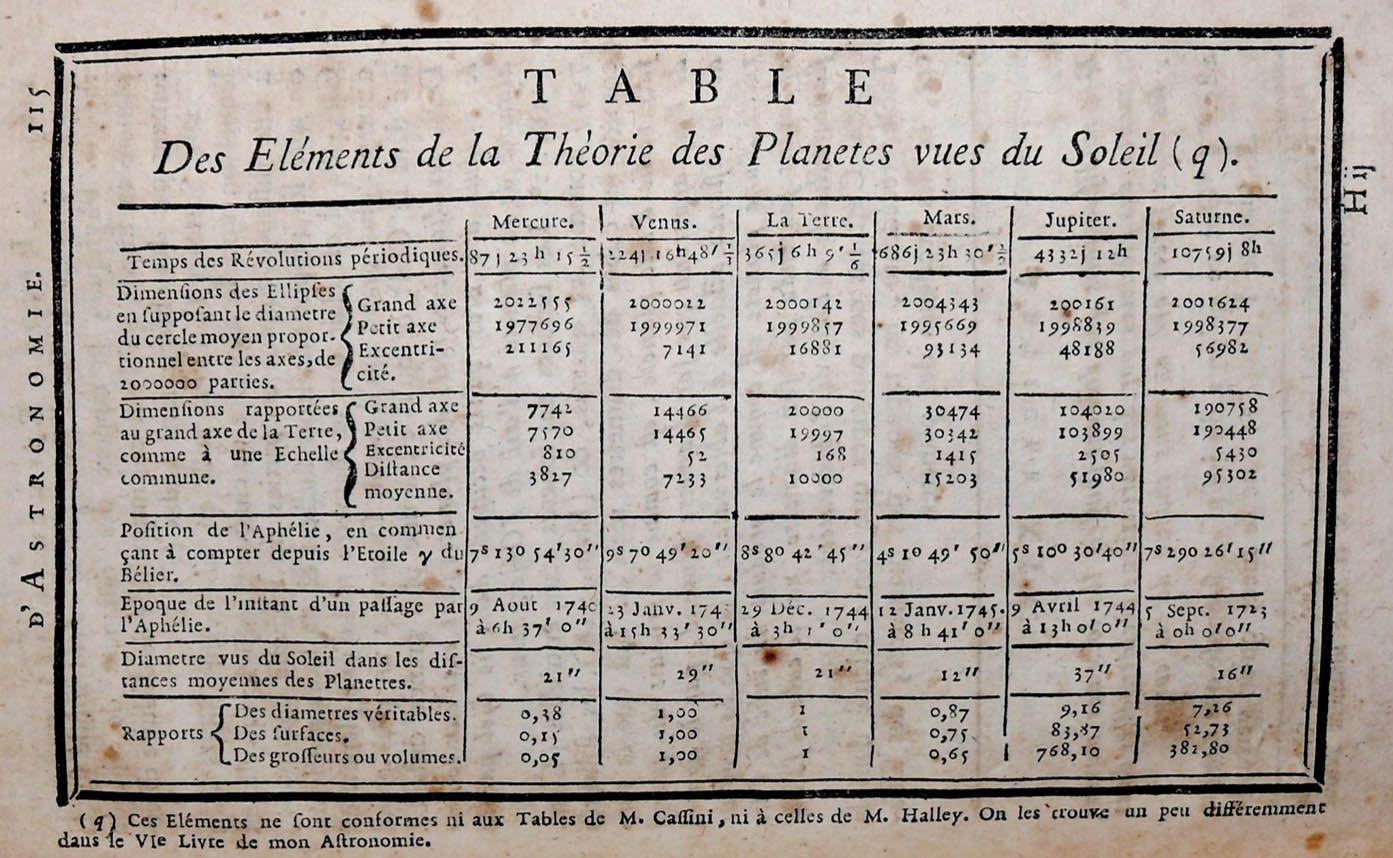
Ce tableau reprend le résultat des calculs de La Caille qui a établi les rapports de distances de chaque planète au Soleil. Il a, pour cela, observé et mesuré les valeurs angulaires des diamètre de chacune d’entre elles, lorsqu’elles se situaient à une distance connue. Son calcul part du principe que: « les diamètres réels des planètes sont entre eux comme le produit des arcs qu’ils occupent dans le ciel par la distance de la planète à l’œil de l’observateur ». La Caille précise cependant la relativité de ses chiffres, expliquant qu’il est parti de l’hypothèse que les trajectoires des planètes étaient régulière, alors qu’il indique par ailleurs que ces dernières peuvent être l’objet de multiples altérations. Montrant quelques exemples de ces variations, il conclue en disant: « Nous ne pouvons pas entrer dans de grands détails sur cet article , qui est le plus compliqué de toute l’astronomie physique.»

Avant de développer, comme le montre cet extrait, son cours sur la mesure du temps, La Caille en explique ainsi les raisons: «La rotation de la Terre sur son axe étant uniforme, les révolutions diurnes des astres autour de la Terre se font en temps égaux; elles sont donc très propres à désigner le temps. Mais comme tous les astres tournent successivement, les uns après les autres et par un mouvement perpétuel, il faut en choisir un seuls qui serve à mesurer le temps par ses révolutions et choisir aussi un terme fixe, pour compter le commencement de chacune de ses révolutions. Or le Soleil est par rapport à la Terre, un astre infiniment plus éclatant que tous les autres ensembles; il parait donc naturel de choisir ses révolutions diurnes pour la mesure du temps, et l’horizon pour le terme de ses révolutions.» Mais comme rien n’est jamais simple en astronomie, La Caille doit ajouter: «Cependant, comme le lever ou le coucher du Soleil ne se font, par rapport à un habitant de la Terre, qu’à l’horizon sensible, qui est un cercle fort irrégulier, rarement confondu avec l’horizon rationnel, souvent entouré de vapeurs qui cachent le Soleil, et qui le défigurent en détournant ses rayons....L’observateur prendra de préférence le méridien pour terme des révolutions diurnes, et pour le premier instant d’un jour, l’instant de midi...»

Dans ce dernier passage, La Caille évoque la nature des influences de la pesanteur de notre satellite. Il en donne deux manifestations: Les marées, sur lesquelles il ne s’étendra pas dans cet ouvrage et qu’il considère comme « étrangères » à l’astronomie et la variation du plan de l’équateur par rapport à celui de l’écliptique, que nous nommons aujourd’hui précession des équinoxes, caractérisée par une variation cyclique de sa valeur entre 22.1° et 24,5°, selon une période d’environ  25.770 années. On notera dans l’extrait ci-dessus que le cycle de 19 ans évoqué par La Caille, à propos de la précession du nœud ascendant de l‘orbite lunaire, n’est autre que l’incidence de la Lune sur la Terre qui a pour conséquence le mouvement de nutation.

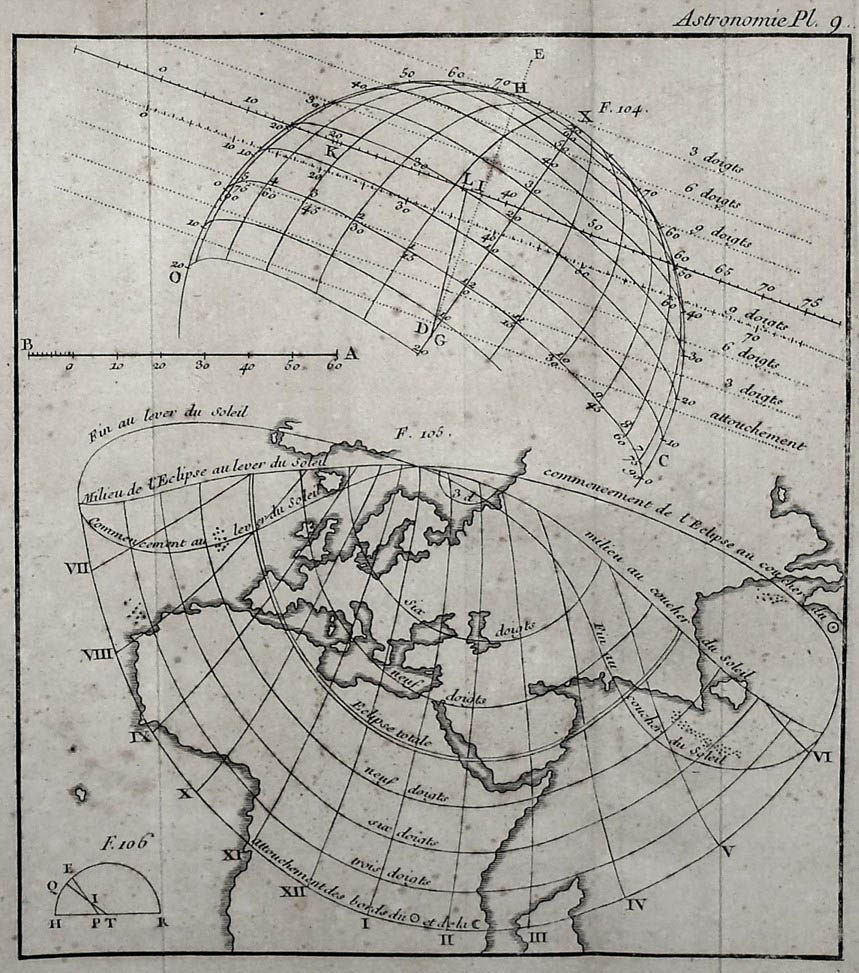
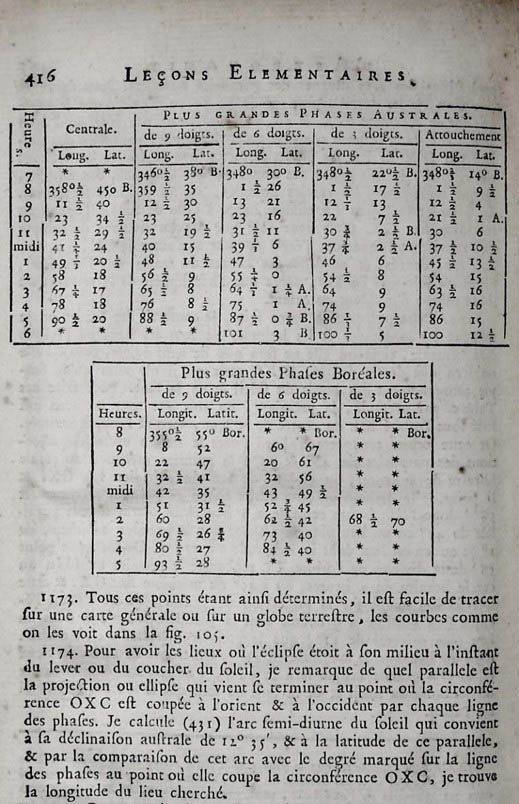
Les figures de la première page ci-dessus (Fig.104 et Fig.105 ci-dessus), illustrent les différentes phases d’une éclipse solaire observée le 26 octobre 1753. Elles ont été tracées à partir du report des valeurs mesurés lors de l’observation et classées dans des tableaux similaires à ceux figurant ci-dessus.