Erathosthène (-276 à -196)
Ératosthène (-276 à -196) est un astronome, géographe, mathématicien et philosophe grec, né à Cyrène, dans l’actuelle Libye. Il vit à Athènes lorsque le pharaon Ptolémée III (Évergète le bienfaiteur) le fait venir en Égypte en tant que précepteur de son fils et qu’il lui confie également la direction de la bibliothèque royale d’Alexandrie. Son immense savoir lui vaut le surnom de Pentathlos, nom du vainqueur des cinq luttes olympiques. Selon Suidas (historien grec du Xème siècle), ayant atteint l’âge de quatre vingt deux ans, Ératosthène perd la vue et, ne supportant plus de ne pouvoir contempler les cieux, cesse de s’alimenter jusqu’à la mort. L’astronomie lui doit énormément. Je ne pourrais décrire ici, tous ses travaux connus, sachons juste que c’est lui qui a engagé Ptolémée III dans le financement de la fabrication d’armilles (cercles de métal), pour observer les mouvements célestes, qu’il a laissé le crible , méthode permettant de déterminer les nombres premiers, qu’il est le premier à tracer une cartographie générale, qu’il écrit une histoire des souverains de Thèbes, qu’il établit un catalogue des étoiles dans lequel il en répertorie six cent soixante quinze, qu’il fait la démonstration de l’inclinaison de l’écliptique… etc. Mais ce sont ses travaux sur la circonférence de la Terre qui ont le plus marqué l’astronomie.
Il effectue le premier une tentative, qualifiable de scientifique, pour déterminer la grandeur de la Terre: on avait depuis longtemps remarqué en Égypte que le jour du solstice d’été, à Syène, les objets ne projetaient aucune ombre et qu’un puits y était éclairé jusqu’au fond, à ce même moment. En d’autre termes, le Soleil était alors situé à la verticale de Syène dont la latitude se trouvait exactement situé sur le tropique. D’autre part, Ératosthène savait qu’à Alexandrie, la distance solsticiale est de 1/50ème de la distance du méridien. L’arc compris entre Syène et Alexandrie est donc de 1/50ème du méridien terrestre (la longitude).
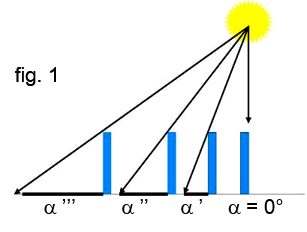
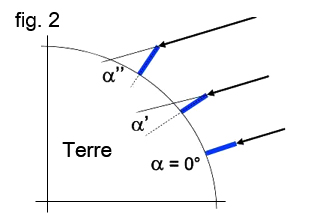Fort de ces données, on peut obtenir les autres dimensions de la Terre en supposant au préalable qu’elle soit sphérique. Ératosthène part du constat initial (voir fig.1) qu’à la verticale d’un lieu il n’y a aucune ombre portée puis, au fur et à mesure qu’on s’éloigne de ce point l’ombre s’agrandit et l’angle qu’elle sous-tend (α) change de valeur (α, α’, α’’). Afin de se rapprocher de la réalité, Ératosthène exploite la solution illustrée par la fig.2, dans laquelle les rayons du Soleil sont entre eux parallèles lorsqu’ils arrivent sur la Terre.
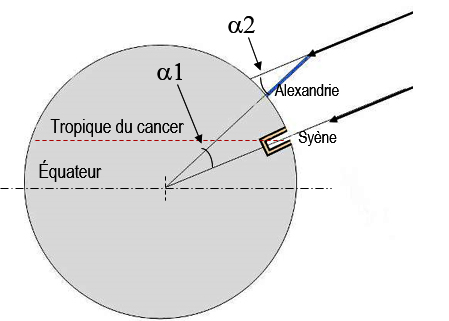Le dernier schéma (ci-contre), reprend la fig.2, transposée en vertu de la règle des angles alternes-internes congrus. Selon cette règle: α1= α2 et l’angle a intercepte l’arc reliant Alexandrie à Syène. Ératosthène connait la taille de cet arc qui n’est autre que la distance séparant les deux villes, soit 5.000 stades (5.000 x 157,5m= 787,5 km). Dés lors il peut calculer la circonférence de la Terre.
Il mesure la valeur de l’angle α2 et trouve 7,2°. Ensuite, sachant que l’arc intercepté (787.5 km) forme un angle de 7,2°, il en déduit qu’une circonférence comprend: 360° : 7,2° = 50 arc (de 7.2°). Il ne lui reste plus qu’à multiplier la distance d’Alexandrie à Syène par le nombre d’arc de 7,2° que contient une circonférence complète soit 50 (nous venons de le voir) pour trouver la circonférence terrestre: 787.5 x 50 = 39 375 km. Ce résultat obtenu avec des moyens rudimentaires se rapproche étonnement de la valeur exacte qui est de 40.075 km. Ces travaux d’Ératosthène sont également symboliques, ils annoncent une nouvelle manière d’aborder l’astronomie et marquent de ce fait l’avènement d’une science qui considérera le monde à portée de l’intelligence humaine.