Aristarque de Samos (-310 à -230)
Aristarque (-310 à -230) est un astronome et mathématicien au sujet duquel nous connaissons très peu d’éléments. Seule une infime partie de son œuvre nous est parvenue, en particulier, grâce à Archimède. Ce qui le distingue, c’est entre autre, qu’il est le premier à avoir calculé la distance de la Terre au Soleil. Pour cela, il a utilisé la méthode de la parallaxe solaire. En préalable il énonce dans son traité Des grandeurs et des distances du soleil et de la lune, les six propositions suivantes, que j’ai reprises en m’inspirant du traité d‘Aristarque de Samos écrit par M. le Comte Fortia d’Urban. (Ed. Firmin Didot.1863).
 1) « La Lune reçoit sa lumière du Soleil ».
1) « La Lune reçoit sa lumière du Soleil ».
2) « La Terre peut être considérée comme un point placé au centre de l’orbite lunaire » Compte tenu des distances en jeu entre la Terre et la Lune, c’est une erreur que de réduire la Terre à un point, car cela signifierait que cette dernière, vue depuis La lune, (ayant un rayon nul: celui d’un point), ne saurait avoir de parallaxe.
3) « Lorsque la Lune nous parait dichotome (coupée en deux parties égales), elle découvre à nos yeux son grand cercle, déterminant sa partie éclairée et sa partie obscure ».
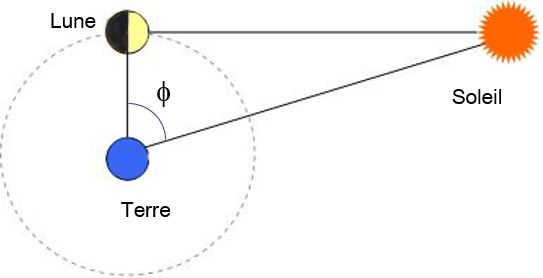
4) « Lorsque la Lune nous parait dichotome, l’angle (f) entre le Soleil et la Lune est moindre du quart de la circonférence ( 90°), de la trentième partie de ce quart: 90° : 30 = 3°, ce qui nous donne : 90° - 3° = 87°. En réalité cet angle a une valeur de 89°50’’ à l’instant de la quadrature ».
5) « La largeur de l’ombre est de deux Lune (4°) ».
6) « L’arc sous-tendu dans le ciel par la Lune, est la quinzième partie d’un signe. Le signe du zodiaque était une unité de mesure qui valait 30° ce qui nous donne pour la Lune un diamètre d’une valeur de 2° (30°: 15 = 2°), soit 4 fois plus que la réalité ».
En partant de ces hypothèse Aristarque va déduire que la distance de la Terre au Soleil, est supérieure de 19 fois (en réalité 400 fois) celle de la Terre à la Lune et inférieure à 20 fois cette même distance. Mais, les hypothèses 2, 4, 5 et 6 étant inexactes, elles fausseront d’autant le résultat final
Il ne faut pas juger trop hâtivement ces résultats à travers le prisme de nos connaissances actuelles. Rappelons-nous qu’à l’époque d’Aristarque, on utilisait pas encore la trigonométrie. Ces mesures interpellent tant leur auteur, qu’il envisage une organisation différente des astres, rompant avec celle communément admise. D’une part, parce qu’il lui parait plus logique que les astres les plus petits gravitent autour des plus gros et non l’inverse, et d’autre part, parce que, ne décelant pas de parallaxe avec les étoiles, il en déduit que c’est en raison de leur trop fort éloignement. Il s’avère qu’il a raison sur ces deux points. Dés lors, l’Univers revêt à ses yeux une toute autre dimension, justifiant ainsi sa proposition d’un système héliocentrique qui lui vaudra, malheureusement, d’être dénoncé aux orthodoxes païens grecs, par le stoïcien Cléanthe qui l’accusa de violer la religion lorsqu’il affirmait que le « foyer » de l’Univers est en mouvement. Son système tombera dans l’oubli, tant il aura été successivement occulté ou combattu, par tous les pouvoirs religieux jusqu’au XVIIème siècle.
On ne sait rien de plus sur la vie d’Aristarque, si ce n’est que Vitruve lui attribue l’invention du scaphion, instrument qui aurait été utilisé pour déterminer le diamètre apparent du Soleil et se serait présenté sous la forme d’une espèce de gnomon recevant l’ombre sur une surface concave hémisphérique portant en son centre l’extrémité du style , de telle sorte que les angles puissent être mesurés directement par des arcs.
Rendons, avant tout, justice à Aristarque à qui nous devons d’être le véritable concepteur du système qui un jour fut attribué à Copernic, non pas parce que ce dernier l’a inventé mais parce qu’il l’a tiré de l’oubli pour lui rendre une place durablement usurpée par le système de Ptolémée.
