Pierre de Maupertuis (1698-1759)
 Pierre Louis Moreau de Maupertuis (1698-1759 ) est le fils ainé d’un père corsaire, anobli par Louis XIV peu avant sa naissance, il voit le jour à Saint Malo. Sa mère, protectrice à l’excès, l’idolâtre au point que son deuxième frère va lui vouer une jalousie maladive. A l’âge de seize ans, il devient pensionnaire au collège Guillaume de Lamarche à Paris où il étudie la philosophie. Au bout de deux ans, sa famille le rappelle à Saint Malo. Il va alors s’initier à la musique, tout en témoignant d’un vif intérêt pour les mathématiques. Comme son père, il aurait pu devenir marin mais sa mère parvient à le dissuader de suivre une carrière qu’elle considère trop dangereuse. Son père lui obtient un poste de lieutenant dans les mousquetaires. Il rejoint son régiment de La Roche Guyon, alors cantonné à Lille. Son poste d’officier, dont auraient rêvé bien des jeunes hommes, ne convenait pas à son tempérament. En 1722, il quitte l’armée pour revenir à Paris et mener une vie davantage agrémentée de joutes intellectuelles que de passes d’armes. Il fréquente un cercle qui se réunit dans des cafés. Il fait la connaissance de Jean Terrasson (philosophe, associé géomètre de l’Académie des sciences), de Joseph Saurin (mathématicien), d’Antoine Houdar de la Mothe (dramaturge) et de l’écrivain, romancier et auteur dramatique Marivaux, avec lequel il se lie d’amitié. A cette époque les cafés jouent un rôle essentiel dans les débats d’idées. Ils offrent un environnement propice, à l’écart des salons aristocratiques. Véritables catalyseurs, ils stimulent et favorisent la diffusion des pensées et voient se révéler certains des plus grands intellectuels que nous donnera le siècle des lumières. C’est dans ce contexte de bouillonnement culturel que Maupertuis affine sa pensée et son savoir scientifiques, en particulier dans le domaine qu’il affectionne, les mathématiques. A vingt cinq ans, il devient adjoint de l’Académie des sciences, l’année suivante il publie un premier article intitulé Sur la forme des instruments de musique, dans lequel il fait la relation entre la forme des instruments et la nature des sons qu’ils produisent. Il publie successivement ses travaux de mathématiques, sur les minimas et maximas, les cycloïdes puis les courbes.
Pierre Louis Moreau de Maupertuis (1698-1759 ) est le fils ainé d’un père corsaire, anobli par Louis XIV peu avant sa naissance, il voit le jour à Saint Malo. Sa mère, protectrice à l’excès, l’idolâtre au point que son deuxième frère va lui vouer une jalousie maladive. A l’âge de seize ans, il devient pensionnaire au collège Guillaume de Lamarche à Paris où il étudie la philosophie. Au bout de deux ans, sa famille le rappelle à Saint Malo. Il va alors s’initier à la musique, tout en témoignant d’un vif intérêt pour les mathématiques. Comme son père, il aurait pu devenir marin mais sa mère parvient à le dissuader de suivre une carrière qu’elle considère trop dangereuse. Son père lui obtient un poste de lieutenant dans les mousquetaires. Il rejoint son régiment de La Roche Guyon, alors cantonné à Lille. Son poste d’officier, dont auraient rêvé bien des jeunes hommes, ne convenait pas à son tempérament. En 1722, il quitte l’armée pour revenir à Paris et mener une vie davantage agrémentée de joutes intellectuelles que de passes d’armes. Il fréquente un cercle qui se réunit dans des cafés. Il fait la connaissance de Jean Terrasson (philosophe, associé géomètre de l’Académie des sciences), de Joseph Saurin (mathématicien), d’Antoine Houdar de la Mothe (dramaturge) et de l’écrivain, romancier et auteur dramatique Marivaux, avec lequel il se lie d’amitié. A cette époque les cafés jouent un rôle essentiel dans les débats d’idées. Ils offrent un environnement propice, à l’écart des salons aristocratiques. Véritables catalyseurs, ils stimulent et favorisent la diffusion des pensées et voient se révéler certains des plus grands intellectuels que nous donnera le siècle des lumières. C’est dans ce contexte de bouillonnement culturel que Maupertuis affine sa pensée et son savoir scientifiques, en particulier dans le domaine qu’il affectionne, les mathématiques. A vingt cinq ans, il devient adjoint de l’Académie des sciences, l’année suivante il publie un premier article intitulé Sur la forme des instruments de musique, dans lequel il fait la relation entre la forme des instruments et la nature des sons qu’ils produisent. Il publie successivement ses travaux de mathématiques, sur les minimas et maximas, les cycloïdes puis les courbes.
Il s’intéresse à la biologie et rédige un traité sur la salamandre dans lequel il révèle d’indéniables talents d’observateur. En 1728, il se rend à Londres où il est élu fellow de la Royal Society (j’ai déjà parlé de ce titre qui désormais était devenu le gage d’une contribution aux connaissances scientifiques). Désireux d’approfondir ses connaissances, Maupertuis se rend à Bâle chez Johann Bernoulli, le mathématicien et physicien Suisse qui le loge. Ce dernier lui explique la théorie des tourbillons de Descartes et la mécanique de Leibniz. Parallèlement, Maupertuis s’intéresse à l’œuvre de Newton. Elle le séduit bien davantage qu’elle ne convient à son maitre qui lui reproche quelques incohérences. Bernoulli, en effet, n’arrive pas à s’expliquer comment deux objets distants, et donc sans liaison mécanique, peuvent interagir entre eux dans le vide. Un an plus tard Maupertuis rentre à Paris et reprend ses études sur les courbes pour publier en 1731 son premier article d’astronomie assorti d’un précis sur les équations différentielles. Cette publication assoie sa réputation de mathématicien même si en 1732, il commet quelques erreurs en publiant dans Les transactions philosophiques » (revue de la Royal Society) un traité émettant l’hypothèse que les anneaux de Saturne pourraient être les restes de la queue d’une comète, retenus par la force d’attraction de la planète. Si cette théorie dénote d’une imagination fertile, elle montre également que Maupertuis n’avait alors pas parfaitement saisi les théories de Newton sur la gravitation. Cela ne l’empêchera pas de se déclarer sans ambigüité en faveur de ce dernier, dans le débat public qui s’ouvre sur cette question. A cette époque, le monde scientifique était partagé en deux groupes. D’une part celui des partisans de Descartes et, d’autre part, ceux qui défendaient les positions de Newton. Selon la théorie des tourbillons cartésiens, la rotation de la Terre sur elle-même lui donnerait une forme allongée et plutôt pointue vers les pôles. Newton croyait, à l’inverse, que la force centrifuge avait un effet contraire et qu’elle faisait enfler la masse terrestre autour de l'équateur, donnant aux pôles une forme plus aplatie. Schématiquement, il s’agissait de défini si la Terre était comparable à une orange ou à un citron. En mai 1735, l’Académie envoie une expédition au Pérou afin d’effectuer des relevés pour servir à déterminer les dimensions de la Terre. Elle est dirigée par Charles Marie de la Condamine et Pierre Bouguer. Une autre mission doit se rendre en Laponie pour effectuer les mêmes mesures. Maupertuis en assurera la direction.
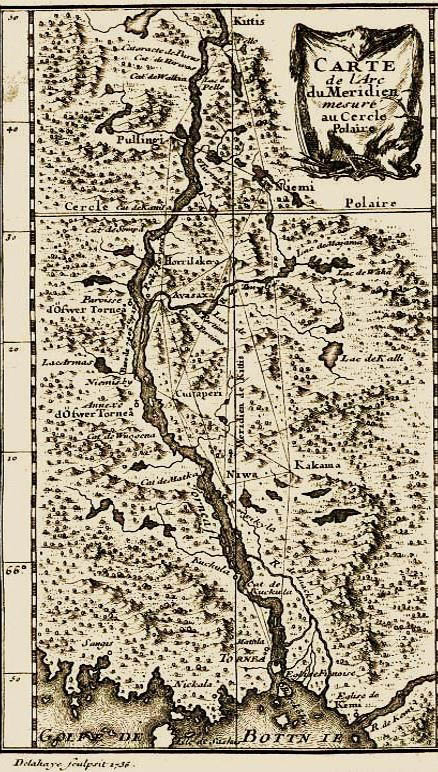 Accompagné par Charles Etienne Louis Camus (mathématicien et astronome), Anders Celsius (scientifique suédois qui donne son nom à l’échelle de températures), Charles Le Monnier et Alexis Claude Clairaut. Il embarque à Dunkerque en mai 1736. Arrivé en Finlande, le groupe installe sa base à Tornka, dans le golf de Bothnie, au nord de la mer Baltique. Ses membres sont logés chez des notables locaux. Ils effectuent les premières mesures aux environs de Noël, affrontant un climat glacial entre - 30° à - 40°C. Ci-contre, la carte des lieux de Tornka jusqu’à Kittis avec la triangulation chevauchant le cercle polaire qui servit au calcul de la portion du méridien.
Accompagné par Charles Etienne Louis Camus (mathématicien et astronome), Anders Celsius (scientifique suédois qui donne son nom à l’échelle de températures), Charles Le Monnier et Alexis Claude Clairaut. Il embarque à Dunkerque en mai 1736. Arrivé en Finlande, le groupe installe sa base à Tornka, dans le golf de Bothnie, au nord de la mer Baltique. Ses membres sont logés chez des notables locaux. Ils effectuent les premières mesures aux environs de Noël, affrontant un climat glacial entre - 30° à - 40°C. Ci-contre, la carte des lieux de Tornka jusqu’à Kittis avec la triangulation chevauchant le cercle polaire qui servit au calcul de la portion du méridien.
Les scientifiques affrontent des conditions climatiques extrêmes, comme en témoignent ces extraits du journal de Maupertuis: « Ce fut le vendredi 21 décembre, jour du solstice d’hiver, jour remarquable pour un pareil ouvrage, que nous commençâmes la mesure de notre base vers « Avasaxa » où elle se trouvait. A peine le Soleil se levait t’il, vers le midi; mais les longs crépuscules, la blancheur des neiges, et le feu dont le ciel est toujours éclairé dans ce pays, nous donnaient chaque jour assez de lumière pour travailler quatre ou cinq heures ... »
« Nous nous rendîmes sur le fleuve avec un tel nombre de traineaux et un si grand équipage, que les Lapons descendirent de leurs montagnes, attirés par la nouveauté du spectacle »…
 « Je ne dirai rien des fatigues, ni des périls de cette opération »… « On imaginera ce que c’est que de marcher dans une neige haute de deux pieds, chargés de perches pesantes, qu’il fallait continuellement poser sur la neige et relever. Pendant un froid si grand, que la langue et les lèvres se gelaient sur le champ contre la tasse, lorsqu’on voulait boire de l’eau de vie, qui était la seule liqueur qu’on pût tenir assez liquide pour la boire, et ne s’en arrachaient que sanglantes; pendant un froid qui gela les doigts de quelques uns de nous, et qui nous menaçait à tout moment d’accidents plus grands encore. Tandis que les extrémités de nos corps étaient glacées, le travail nous faisait suer. L’eau de vie ne put suffire à nous désaltérer, il fallut creuser dans la glace, des puits profonds, qui étaient presque aussitôt refermés, et d’où l’eau pouvait à peine parvenir liquide à la bouche. Et il fallait s’exposer au dangereux contraste, que pouvait produire dans nos corps échauffés, cette eau glacée »…« Cependant l’ouvrage avançait, six journées de travail l’avaient conduit au point, qu’il ne restait plus qu’à mesurer environ 500 toises, qui n’avaient pas pu être remplies de piquets assez tôt ». Conditions limites pour effectuer un travail de précision, dont nos mathématiciens et astronomes habitués au travail en laboratoire ou aux salles de l’Académie allaient s’acquitter avec un courage remarquable qui vaudra bien la reconnaissance qu’ils en reçurent.
« Je ne dirai rien des fatigues, ni des périls de cette opération »… « On imaginera ce que c’est que de marcher dans une neige haute de deux pieds, chargés de perches pesantes, qu’il fallait continuellement poser sur la neige et relever. Pendant un froid si grand, que la langue et les lèvres se gelaient sur le champ contre la tasse, lorsqu’on voulait boire de l’eau de vie, qui était la seule liqueur qu’on pût tenir assez liquide pour la boire, et ne s’en arrachaient que sanglantes; pendant un froid qui gela les doigts de quelques uns de nous, et qui nous menaçait à tout moment d’accidents plus grands encore. Tandis que les extrémités de nos corps étaient glacées, le travail nous faisait suer. L’eau de vie ne put suffire à nous désaltérer, il fallut creuser dans la glace, des puits profonds, qui étaient presque aussitôt refermés, et d’où l’eau pouvait à peine parvenir liquide à la bouche. Et il fallait s’exposer au dangereux contraste, que pouvait produire dans nos corps échauffés, cette eau glacée »…« Cependant l’ouvrage avançait, six journées de travail l’avaient conduit au point, qu’il ne restait plus qu’à mesurer environ 500 toises, qui n’avaient pas pu être remplies de piquets assez tôt ». Conditions limites pour effectuer un travail de précision, dont nos mathématiciens et astronomes habitués au travail en laboratoire ou aux salles de l’Académie allaient s’acquitter avec un courage remarquable qui vaudra bien la reconnaissance qu’ils en reçurent.
Maupertuis a dirigé ses mesures sans rien négliger, il l’évoque ainsi: « J’avais consulté Mr Bradley pour savoir s’il avait quelques observations immédiates des deux étoiles dont nous nous sommes servis pour déterminer l’amplitude de notre arc. Il a bien voulu me faire part de ses dernières découvertes sur l’aberration, et sur ce troisième mouvement des étoiles. La correction qu’il m’a envoyée pour notre amplitude, dans laquelle il a eu égard à la précession des équinoxes, à l’aberration de la lumière, et à ce mouvement nouveau ne diffère pas sensiblement de la correction que nous avons faite pour la précession et l’aberration seulement; comme on le verra dans le détail de nos opérations. Quoiqu’on puisse donc assez sûrement compter sur la correction pour l’aberration de la lumière, nous voulions tâcher que cette correction fût peu considérable; pour satisfaire ceux (s’il y en a) qui ne voudraient pas encore admettre la théorie de M. Bradley, ou qui croiraient qu’il y a quelqu’autre mouvement dans les étoiles: il fallait pour cela que le temps qui s’écoulerait entre les observations de Kittis et celles de Tornea, fut le plus court qu’il serait possible ». Les relevés du groupe de Maupertuis permirent d’établir l’aplatissement de la Terre à proximité des Pôles et aboutit à créer un conflit avec Cassini qui réfutait les idées de Newton à ce sujet. Durant les longues nuits de l’hiver nordiques, Maupertuis est tombé amoureux d’une Lapone qu’il ramène avec lui à Paris et exhibe dans les salons où il affectionne à se montrer, en ayant cesse de vanter les qualités d’amante de sa jeune compagne. En 1738, Il publie le compte rendu de ses observations dans La figure de la terre. Il avait auparavant entretenu des relations avec Émilie du Chatelet, qui travaillait alors sur sa traduction des Principia de Newton. Désireuse de se perfectionner en mathématiques, elle avait fait appel à Maupertuis. A cette occasion, leur relation avait dépassé le cadre scientifique puisque la marquise était devenu sa maîtresse. Émilie du Chatelet lui préféra cependant Voltaire, avec qui elle vivait une passion intellectuelle plus que charnelle. Il s’en suivra une brouille entre les deux hommes, qui éclatera lorsque Maupertuis, grisé par les mondanités, délaisse ses travaux de scientifique et se rabaisse auprès des grands pour obtenir leurs faveurs. Il est invité à Berlin à la cour de Fréderic II. En 1750, Voltaire résidait à sa Cour avec la fonction de chambellan, pour laquelle il recevait un traitement confortable. Il entretenait même une relation amicale avec ce roi amoureux de philosophie et de littérature. Mais assez vite, l’attitude altière du souverain habitué à un public soumis se heurte à la supériorité intellectuelle de Voltaire. La brouille se profile. Inévitable, elle éclate en 1753, lorsque le souverain soutient Maupertuis lors d’un différent qui l‘oppose à Voltaire. Ce dernier quitte Berlin, alors qu’on attaque violemment son dernier roman Micromégas qui raconte l’histoire d’un être qui réside sur une planète de l’étoile Sirius et descend visiter la Terre en compagnie d’un de ses amis, secrétaire de l'Académie de Saturne. Maupertuis comprendra plus tard que Fréderic II, en le nommant président de l’Académie des Sciences de Berlin en 1642, l’avait attiré par intérêt. Il avait, à dessein, flatté son égo démesuré afin qu’il contribua au rayonnement de l’académie prussienne. Le monarque cultivait l’ambition de voir son institution rayonner au premier rang des académies européennes. J’évoque ces péripéties qui s’éloignent de l’astronomie car elles soulignent à quel point en ce XVIIIème siècle, les passions transformaient de simples divergences d’opinion en de violents affrontement intellectuels. Une révolution était en marche qui n’allait pas s’arrêter de si tôt. Pour achever ma digression, je voulais enfin citer Maupertuis, le philosophe, qui renvoie dos à dos la mécanique cartésienne et l'attraction de Newton. Suivant leurs auteurs, elles suffisent à expliquer notre monde dans lequel, les parties les plus infimes de la matière se meuvent uniformément. Maupertuis les réfute en abordant l’existence même de la vie; il explique que ces parties les plus petites de matière vivante de l'embryon, suivent une évolution différente selon les différents organes qu'elles vont former; il s’exprime ainsi: « Si toutes ont la même tendance, la même force pour s'unir les unes aux autres, pourquoi celles-ci vont-elles former l'œil, pourquoi celles-là l'oreille ? Pourquoi ce merveilleux arrangement ? ». Pour répondre à cette question il faut, selon lui, admettre que la matière dispose de propriétés supplémentaires. Il attribue des propriétés psychiques à la matière vivante pour expliquer la formation des corps organisés. Mais il va plus loin, lorsqu’il évoque le désir et la mémoire. Il suppose que les molécules (terme utilisé pour décrire les plus petites parties constituant la matière vivante), elles-mêmes, doivent être « conscientes ». Il leur attribue un degré infinitésimal de « perception » ou « sensibilité », qui entraîne une « conscience minimale de soi ». Alors que pour Descartes, tous les corps, vivants ou non, sont inertes, que leurs processus vitaux ne sont que des mouvements mécaniques, que chacun de leur mouvement leur est donné de l'extérieur et qu’enfin, les corps ne sont que des automates. Maupertuis rétorque, non sans égratigner Newton: « Tout sentiment, toute perception est une pensée. Elle est nécessairement accompagnée du sentiment de soi, de ce que les Philosophes appellent conscience... Or c'est ce sentiment du soi qui caractérise la simplicité et l'indivisibilité de la substance à laquelle il appartient : ainsi le sentiment le plus léger ou le plus confus, qu'aurait une huître, suppose autant une substance simple et indivisible que les spéculations les plus sublimes et les plus compliquées de Newton ».
