Joseph Louis Lagrange (1736-1813)

Guiseppe Lodovico (Joseph Louis) Lagrangia (1736-1813) est né à Turin. Sa mère Teresa Grosso est italienne, fille d’un riche médecin de Cambiano dans le Piémont et son père Giuseppe Francesco, d’origine française est trésorier au bureau des travaux publics et des fortifications de la ville de Turin. Lagrange est l’ainé d’une famille de onze enfants, dont neuf n’atteignirent pas l’âge adulte. Le père de Joseph Louis occupait un poste important dans l’administration du roi de Sardaigne (Turin dépendait alors du duc de Savoie, également roi de Sardaigne), mais sa famille n’en bénéficia pas vraiment, car elle perdit de grosses sommes d’argent dans des spéculations financières douteuses. La famille de Joseph Louis le destine à devenir homme de loi. Le jeune homme semble se résigner à cette perspective. Il étudie au collège de Turin où le latin est sa matière favorite. Initialement, il ne se montra pas particulièrement brillant pour l’étude des mathématiques et en particulier celle de la géométrie. Alors qu’il suit les cours de physique de Giambattista Beccaria (qui sera le premier à installer un paratonnerre de Franklin en Italie), Lagrange tombe sur une publication de Edmund Halley dans les Philosophical transactions, qui explique comment exploiter les mathématiques dans les calculs relatifs à l’optique. Montrant un vif intérêt pour ces travaux et, en phase avec les principes de la méthode analytique, il décide qu’il se consacrera à l’études approfondie des mathématiques. En deux années entièrement dédiées à cette matière, il atteint un niveau digne des meilleurs mathématiciens de son temps. Il écrit alors à Léonard Euler, considéré comme le plus éminent d’entre eux, pour lui proposer ses idées au sujet d’une méthode d’analyse fonctionnelle supposée résoudre les problèmes iso périmétriques, connus aujourd’hui sous le nom de calcul de variations. Euler montre beaucoup d’attention pour les propositions du jeune Lagrange, au point de retarder une de ses propres publications sur le sujet. A l’âge de 19 ans seulement, Lagrange est nommé professeur de géométrie à l’École d’artillerie. Adoubé par Euler, il devient membre de l’Académie de Berlin en 1756. Avec ses amis, le comte Giuseppe Angelo Saluzzo et Giovanni Francesco Cigna, respectivement chimiste et physicien, il fonde en 1757 une société savante qui deviendra deux ans plus tard l’Académie des sciences de Turin.

La première publication de cette institution, Recherche sur la nature et la propagation du son, est écrite par Lagrange. De 1764 à 1768, il remporte cinq années consécutives le prix de mathématiques de l’Académie de Paris. Pour son prix de l’année 1764, Jean Le Rond D’Alembert lui écrit pour le féliciter des réponses qu’il avait apportées au problème concernant la libration de la lune. Lagrange, âgé de vingt huit ans se rend à Paris où Clairaut et d’Alembert le reçoivent. A son retour à Turin, il est informé qu’il vient de remporter de nouveau un prix, cette fois pour sa théorie sur les satellites de Jupiter. Considérant les interactivités gravitationnelles du Soleil, de la planète et des satellites joviens, il a trouvé les équations différentielles qui caractérisent leurs mouvements. Sur recommandation de d’Alembert et de Euler, il est nommé directeur de l’Académie des sciences de Berlin. Il quitte alors Turin et réside à Berlin jusqu’en 1786, tandis que Mirabeau, l’homme de plume, écrit à propos de Lagrange: « Le premier géomètre qui ait paru depuis Newton et qui, sous tous les rapports de l'esprit et du génie, est l'homme qui m'a le plus étonné ; le plus sage et peut-être le seul philosophe qui ait existé »,  Mirabeau le diplomate, officieusement envoyé à Berlin, tente de convaincre Lagrange de venir à Paris. Le roi Louis XVI lui propose une pension confortable. En 1787, Lagrange arrive à Paris; l’année suivante, il devient directeur de l’Académie des sciences. La révolution vient d’éclater, Lagrange fait preuve de prudence et ne se range du côté d’aucun mouvement d’opinion, préférant se consacrer à son travail de mathématicien. Le comité révolutionnaire de salut public ayant supprimé les activités de l’Académie en 1793, avait parallèlement mis en place une Commission temporaire des Poids et Mesures. Lagrange allait jouer un rôle au sein de cette commission, qui avait la charge de mettre au point un système général de poids et de mesures. Ses collègues, en revanche, furent victimes de la répression révolutionnaire. Ainsi en raison des idées politiques qu’ils avaient exprimées, Lavoisier et Bailly furent décapités, Condorcet mourut en prison, Coulomb dut abandonner tous ses biens pour aller se réfugier à Blois, chez Borda et Laplace, adversaires de la dictature.

Malgré sa neutralité effective, Lagrange tomba sous le coup d’une loi promulguée en 1793, qui interdisait tout étranger à résider en France. Ayant conscience de la perte que représenterait son départ, le chimiste Louis Bernard Guyton de Morveau, devenu Guyton-Morveau, membre du Comité de Salut Public et le mathématicien Gaspard Monge, ami de Robespierre, protégèrent Lagrange en faisant adopter un arrêté par lequel il était réquisitionné pour continuer des calculs sur la théorie du mouvement des projectiles. Le 21 décembre 1794 (1^er Nivôse de l’an III), Lagrange préside l’inauguration de l’École Polytechnique. La première rentrée voit arriver à l'École près de quatre cents élèves de niveaux scolaires différents. Un premier cycle de trois mois appelé  « cours révolutionnaires » permet de répartir les élèves en trois niveaux: ceux qui peuvent immédiatement entrer dans les services publics de l'État, ceux qui n'ont besoin que d'une année de formation avant d'entrer dans les écoles des services publics et ceux qui doivent suivre deux ans de cours. Lagrange ne prendra pas part, comme les autres « instituteurs », aux cours révolutionnaires.

Dans son travail de mathématicien, une de ses contributions la plus importante pour l’astronomie, est illustrée par la découvertes des « points » dit de Lagrange. Ses « points » définissent un cas particulier du problème à trois corps, où l'un des trois corps est de masse négligeable devant les deux autres. Ces « points » sont au nombre de cinq ( L1 à L5), dans le système illustré par le schéma ci-dessous à droite, qui représente l’ensemble Terre / Soleil.

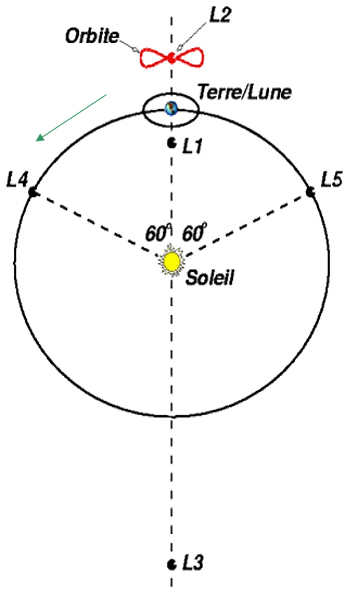Dans un système où évoluent deux corps, un point de Lagrange est une position donnée, située en un lieu où les forces gravitationnelles de ces deux corps se combinent de telle manière qu’il soit un point d’équilibre pour un troisième corps de masse négligeable, tel que les positions relatives des trois corps soient fixes.

Sur le schéma, les points de Lagrange sont ceux où ce corps, soumis aux attractions conjuguées du Soleil et de la Terre, suit une orbite autour du Soleil, à la même vitesse angulaire que la Terre. Les lieux L1 et L2 se situent à proximité de la Terre et répondent à la loi définie par un rapport des distances, proportionnel à la racine cubique du rapport des masses. Le point L3, correspond au point de symétrie avec la Terre, par rapport au Soleil. Les points L4 et L5 sont les sommets de triangles équilatéraux ayant pour base la distance Soleil / Terre.

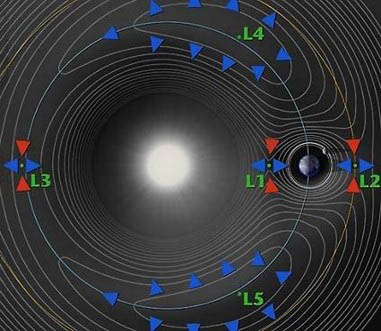
Le deuxième schéma ci dessous montre, d’une autre manière, les lignes gravitationnelles et la répartition des points de Lagrange par rapport à ces lignes de forces. Les équations de Lagrange montrent que seules les orbites autour des points L4 et L5 sont stables. Les autres, autour de  L1, L2 et L3 sont instables en raison de la force de Coriolis (en rouge sur le schéma de gauche, on peut voir l’incidence de la force de Coriolis sur l’orbite de L2).

Les conséquences de la découverte de ces points présentant des propriétés gravitationnelles particulières sont exploitées de nos jours pour déterminer la position des satellites. Ainsi, le satellite SOHO, dédié à l’étude du Soleil, positionné en L1, reste toujours en face de celui-ci, tout en accompagnant la Terre dans sa révolution. Le satellite JWST qui remplacera Hubble pour étudier l’univers froid, sera positionné en L2, ce qui lui permettra de viser les profondeurs sidérales, sans être perturbé par le Soleil qui sera toujours dans une position opposée à sa ligne de visée.

Les travaux de Lagrange ont donc encore des répercussions directes sur les programmes spatiaux actuels. L’astronomie lui doit autant qu’à Galilée ou à Newton. Ses recherches en mathématiques ont exploré de multiples aspects de cette discipline, au point qu’aujourd’hui, le nom de Lagrange demeure omniprésent, à travers ses théorèmes, équations et autres formules. La France lui a témoigné sa reconnaissance en l’inscrivant durablement dans son histoire. Sa dépouille repose au Panthéon, au côtés des plus grands hommes de la nation.