James Bradley (1693-1762)
 James Bradley (1693-1762) est né à Sherborne dans la province de Gloucester en Angleterre. Il suit des études ordinaires et ne parait pas être un élève particulièrement doué. C’est alors qu’il contracte la petite vérole (variole) et qu’il est soigné par son oncle maternel James Pound, prêtre, astronome amateur et ami de Halley et de Newton. Pound qui s’était fait remarquer pour ses mesures des distances des satellites à leurs planètes principales, ne tarde pas à faire partager à son neveu sa passion pour l’astronomie. A 18 ans, Bradley entre au Balliol Collège d’Oxford pour y étudier la théologie. Il s’initie parallèlement aux sciences physiques et effectue quelques observations astronomiques dont il présente les comptes rendus à la Royal Society entre 1717 et 1718. Devenu aumônier de l’évêque de Hertford sous la pression familiale, il démissionne de ce poste sans regret pour occuper une chaire d‘astronomie à Oxford. Sa carrière n’aurait pas connu un tel succès, s’il ne s’était trouvé confronté à une question d’astronomie non élucidée. Picard avait effectivement remarqué, en observant l’étoile polaire, que cette dernière était animée d’un mouvement singulier pour lequel il ne trouva aucune loi ou explication satisfaisante. Il nota simplement que « l’inégalité allait jusqu’à une valeur de 40’’ et se rétablissait tous les ans ». Il avait cru y voir une parallaxe, tout comme Flamsteed qui se pencha à son tour sur la question. Mais Cassini montra qu’il n’en était rien, sans pour autant pouvoir donner à ce phénomène une explication convenable. Samuel Molyneux, astronome, ami de Bradley et spécialiste d’optique, avait lu les écrits de Picard et établi les caractéristiques idéale d’une lunette destiné à la mesure des angles. A ces fins, il dota son observatoire, situé à Kew, au sud-ouest de Londres, d’un secteur zénithal (ci-dessous) fabriqué par le célèbre constructeur George Graham et dédié à la mesure des variations angulaires.
James Bradley (1693-1762) est né à Sherborne dans la province de Gloucester en Angleterre. Il suit des études ordinaires et ne parait pas être un élève particulièrement doué. C’est alors qu’il contracte la petite vérole (variole) et qu’il est soigné par son oncle maternel James Pound, prêtre, astronome amateur et ami de Halley et de Newton. Pound qui s’était fait remarquer pour ses mesures des distances des satellites à leurs planètes principales, ne tarde pas à faire partager à son neveu sa passion pour l’astronomie. A 18 ans, Bradley entre au Balliol Collège d’Oxford pour y étudier la théologie. Il s’initie parallèlement aux sciences physiques et effectue quelques observations astronomiques dont il présente les comptes rendus à la Royal Society entre 1717 et 1718. Devenu aumônier de l’évêque de Hertford sous la pression familiale, il démissionne de ce poste sans regret pour occuper une chaire d‘astronomie à Oxford. Sa carrière n’aurait pas connu un tel succès, s’il ne s’était trouvé confronté à une question d’astronomie non élucidée. Picard avait effectivement remarqué, en observant l’étoile polaire, que cette dernière était animée d’un mouvement singulier pour lequel il ne trouva aucune loi ou explication satisfaisante. Il nota simplement que « l’inégalité allait jusqu’à une valeur de 40’’ et se rétablissait tous les ans ». Il avait cru y voir une parallaxe, tout comme Flamsteed qui se pencha à son tour sur la question. Mais Cassini montra qu’il n’en était rien, sans pour autant pouvoir donner à ce phénomène une explication convenable. Samuel Molyneux, astronome, ami de Bradley et spécialiste d’optique, avait lu les écrits de Picard et établi les caractéristiques idéale d’une lunette destiné à la mesure des angles. A ces fins, il dota son observatoire, situé à Kew, au sud-ouest de Londres, d’un secteur zénithal (ci-dessous) fabriqué par le célèbre constructeur George Graham et dédié à la mesure des variations angulaires.
 Les premiers relevés de Molyneux débutent en 1725 sur l’étoile Eltanin (γ du dragon), choisie en raison de sa faible distance au zénith qui n’est que de quelques minutes, ce qui minimise ainsi les irrégularités crées par la réfraction. Elles montrent que les variations de position de l’étoile sont, d'une part beaucoup trop grandes et, d'autre part, orthogonales au mouvement prévu. C’est alors que Bradley s’intéresse à cette énigme et rejoint son ami pour entamer avec lui une longue série d’observations qui confirmeront que la position apparente de l'étoile ne s'est pas déplacée dans le sens attendu. Lorsque Molyneux est nommé à l’amirauté, Bradley doit quitter l’observatoire de ce dernier. Il va cependant poursuivre le travail en cours à l'aide d'une lunette moins performante, de taille inférieure, dotée d’un système optique à large champ, qu’il installe dans la maison de sa tante. Il observe alors assidument l’étoile et note sa dérive au fil du temps. Au bout d’un an, le tracé des positions successives de l’étoile forme une petite ellipse. Bradley, modeste, commente alors : « J’ai seulement observé les changements dans la déclinaison apparente des étoiles ». Ces changements désormais identifiés dans le temps et en amplitude ne peuvent s’expliquer ni par la parallaxe annuelle ni par la nutation de l’axe de la Terre, dont l’amplitude n’est que de l’ordre d’une fraction de seconde, alors que les écarts notés par Bradley avoisinent trente neuf secondes. Il entreprend d’étendre ses mesures à d’autres étoiles. Il rend compte de ses travaux dans les transactions philosophiques en 1728. Il dégage une règle qui justifie ces différences énigmatiques et il trouve une formule qui les définit à partir de ce qu’il nomme l’ellipse d’aberration. Il la nomme tout naturellement aberration de déclinaison . Descartes avait annoncé que, si la vitesse de la lumière n’était pas instantanée, nous ne verrions jamais les astres et les planètes dans le lieu qu’elles occupent réellement. Il cherchait en fait, en s’appuyant sur les tables astronomiques, à démontrer que les astres sont toujours vus dans le lieu qu’ils occupent réellement et donc que la vitesse de la lumière était infiniment grande. Il faisait évidement une erreur sur ce point.
Les premiers relevés de Molyneux débutent en 1725 sur l’étoile Eltanin (γ du dragon), choisie en raison de sa faible distance au zénith qui n’est que de quelques minutes, ce qui minimise ainsi les irrégularités crées par la réfraction. Elles montrent que les variations de position de l’étoile sont, d'une part beaucoup trop grandes et, d'autre part, orthogonales au mouvement prévu. C’est alors que Bradley s’intéresse à cette énigme et rejoint son ami pour entamer avec lui une longue série d’observations qui confirmeront que la position apparente de l'étoile ne s'est pas déplacée dans le sens attendu. Lorsque Molyneux est nommé à l’amirauté, Bradley doit quitter l’observatoire de ce dernier. Il va cependant poursuivre le travail en cours à l'aide d'une lunette moins performante, de taille inférieure, dotée d’un système optique à large champ, qu’il installe dans la maison de sa tante. Il observe alors assidument l’étoile et note sa dérive au fil du temps. Au bout d’un an, le tracé des positions successives de l’étoile forme une petite ellipse. Bradley, modeste, commente alors : « J’ai seulement observé les changements dans la déclinaison apparente des étoiles ». Ces changements désormais identifiés dans le temps et en amplitude ne peuvent s’expliquer ni par la parallaxe annuelle ni par la nutation de l’axe de la Terre, dont l’amplitude n’est que de l’ordre d’une fraction de seconde, alors que les écarts notés par Bradley avoisinent trente neuf secondes. Il entreprend d’étendre ses mesures à d’autres étoiles. Il rend compte de ses travaux dans les transactions philosophiques en 1728. Il dégage une règle qui justifie ces différences énigmatiques et il trouve une formule qui les définit à partir de ce qu’il nomme l’ellipse d’aberration. Il la nomme tout naturellement aberration de déclinaison . Descartes avait annoncé que, si la vitesse de la lumière n’était pas instantanée, nous ne verrions jamais les astres et les planètes dans le lieu qu’elles occupent réellement. Il cherchait en fait, en s’appuyant sur les tables astronomiques, à démontrer que les astres sont toujours vus dans le lieu qu’ils occupent réellement et donc que la vitesse de la lumière était infiniment grande. Il faisait évidement une erreur sur ce point.
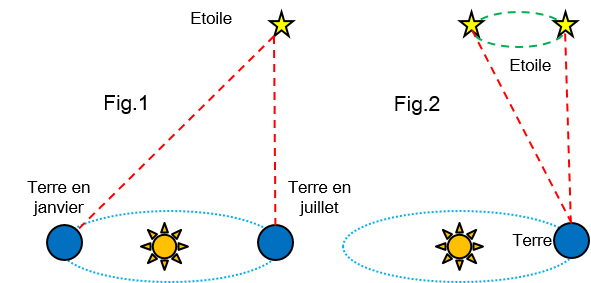 La fig.1 montre le mouvement annuel de la Terre autour du Soleil. De ce fait, un observateur terrestre qui observerait l’étoile représentée ici en jaune, pourrait la voir décrire une ellipse. Ce mouvement relatif est montré sur la figure 2. Il ne définit pas le mouvement réel de cette étoile mais sa trajectoire apparente (en vert) au cours de l’année lorsqu’elle est observée depuis un point de la Terre. Pour comprendre les raisons du phénomène décrit par ce dernier croquis, Bradley s’appuie sur les travaux de Römer. En effet l’aberration qu’il met en évidence est liée à la vitesse de la lumière. Si cette dernière avait été infinie, aucune aberration ne serait apparue. Bradley confirme donc, à son tour, que la lumière a bien une vitesse finie. Ses observations lui permettent de montrer que la lumière met 8 mn et 12’’ pour venir du Soleil à la Terre. Ce qui correspond à une vitesse 295.000 Km/s. (+ ou – 5.000 km/s.)
La fig.1 montre le mouvement annuel de la Terre autour du Soleil. De ce fait, un observateur terrestre qui observerait l’étoile représentée ici en jaune, pourrait la voir décrire une ellipse. Ce mouvement relatif est montré sur la figure 2. Il ne définit pas le mouvement réel de cette étoile mais sa trajectoire apparente (en vert) au cours de l’année lorsqu’elle est observée depuis un point de la Terre. Pour comprendre les raisons du phénomène décrit par ce dernier croquis, Bradley s’appuie sur les travaux de Römer. En effet l’aberration qu’il met en évidence est liée à la vitesse de la lumière. Si cette dernière avait été infinie, aucune aberration ne serait apparue. Bradley confirme donc, à son tour, que la lumière a bien une vitesse finie. Ses observations lui permettent de montrer que la lumière met 8 mn et 12’’ pour venir du Soleil à la Terre. Ce qui correspond à une vitesse 295.000 Km/s. (+ ou – 5.000 km/s.)
 Je reprends ici l’anecdote que relate Ferdinand Hoeffer dans son Histoire de l’astronomie publiée en 1873: « Bradley se promenait un jour sur la Tamise. Le bateau à voile qu'il montait, glissait rapidement à la surface du fleuve, lorsque tout a coup ses yeux se fixèrent sur un phénomène qui aurait semblé vulgaire à tout autre qu'à Bradley; chaque fois que le bateau tournait pour s'approcher ou s'éloigner du rivage, la petite girouette que portait le sommet du mat se mettait a osciller, comme s'il y avait eu un changement dans la direction du vent. Bradley vit d'abord, sans rien dire, ce phénomène se reproduire trois ou quatre fois. Enfin il rompit le silence et témoigna aux marins sa surprise de constater une régularité aussi constante dans la direction du vent, chaque fois que le bateau virait de bord. « Ce n'est pas le vent. qui change ainsi, lui répondirent les mariniers; c‘est la direction différente du bateau qui détermine toujours ce changement apparent. »… « Cette réponse fut pour lui une révélation: le mouvement combiné du bateau et du vent le fit songer au mouvement combiné de la Terre et de la lumière lancée du Soleil; car à cette époque les observations du Römer sur les éclipses des satellites de Jupiter avaient déjà fait connaitre la vitesse de la lumière, estimée environ dix mille fois plus grande que celle du mouvement de translation de la Terre. Or cette différence suffisait pour expliquer les petits déplacements stellaires, en les attribuant au mouvement de translation de la Terre, combiné avec celui de la lumière des étoiles. Voila comment Bradley fut conduit a découvrir, en septembre 1728, la cause de l'aberration ». Bradley explique sa découverte en soulignant que toute information lumineuse reçue à l’instant « t » d’un astre situé à une distance « d » de la Terre fut en réalité émise à l’instant (t – d / 300.000), alors que cet astre occupait une position autre sur la voûte céleste. La différence entre la position apparente et la position réelle de cet astre sera d’autant plus importante que l’objet visé est éloigné. Bradley revint sur les observations de Picard dont les fréquents déplacements lui avaient interdit d’effectuer des observations suivies, mais qui avait cependant noté que sur une durée de dix années, une autre cause inconnue avait souvent changé les résultats, sans rendre pourtant la période méconnaissable. Bradley analysa ces données et les recoupa avec ses propres mesures. Il s’aperçut que cette « complication » qui avait interpellé Picard, évoluait suivant un cycle de dix huit ans (comme celle des nœuds de la Lune). Il devenait clair pour Bradley qu’il était en présence d’une nutation de la Terre sur son axe. Bradley attendit 1748 pour publier ses conclusions. Grace à ces deux découvertes, l’astronomie devenue « moderne » allait pouvoir réaliser des progrès considérables. En 1741, Bradley succède à Halley à l’Observatoire Royal. Le roi lui confie le vicariat de Greenwich, qu’il refuse, tant il craint que cette nouvelle charge ne viennent perturber ses travaux d’astronome. Bradley sera également un des huit associés étrangers de l’Académie des sciences de Paris à partir de 1748. Il obtiendra la médaille Copley (médaille la plus prestigieuse attribuée par la Royal Society). Ce n’est étonnement qu’en 1752 qu’il sera enfin admis au sein de cette académie. En tant qu’un des principaux promoteurs du calendrier Grégorien en Angleterre, il faillit être lapidé par une population de fanatiques opposants. Il mourut à l’âge de soixante-douze ans, au terme de deux années de souffrance et de maladie.
Je reprends ici l’anecdote que relate Ferdinand Hoeffer dans son Histoire de l’astronomie publiée en 1873: « Bradley se promenait un jour sur la Tamise. Le bateau à voile qu'il montait, glissait rapidement à la surface du fleuve, lorsque tout a coup ses yeux se fixèrent sur un phénomène qui aurait semblé vulgaire à tout autre qu'à Bradley; chaque fois que le bateau tournait pour s'approcher ou s'éloigner du rivage, la petite girouette que portait le sommet du mat se mettait a osciller, comme s'il y avait eu un changement dans la direction du vent. Bradley vit d'abord, sans rien dire, ce phénomène se reproduire trois ou quatre fois. Enfin il rompit le silence et témoigna aux marins sa surprise de constater une régularité aussi constante dans la direction du vent, chaque fois que le bateau virait de bord. « Ce n'est pas le vent. qui change ainsi, lui répondirent les mariniers; c‘est la direction différente du bateau qui détermine toujours ce changement apparent. »… « Cette réponse fut pour lui une révélation: le mouvement combiné du bateau et du vent le fit songer au mouvement combiné de la Terre et de la lumière lancée du Soleil; car à cette époque les observations du Römer sur les éclipses des satellites de Jupiter avaient déjà fait connaitre la vitesse de la lumière, estimée environ dix mille fois plus grande que celle du mouvement de translation de la Terre. Or cette différence suffisait pour expliquer les petits déplacements stellaires, en les attribuant au mouvement de translation de la Terre, combiné avec celui de la lumière des étoiles. Voila comment Bradley fut conduit a découvrir, en septembre 1728, la cause de l'aberration ». Bradley explique sa découverte en soulignant que toute information lumineuse reçue à l’instant « t » d’un astre situé à une distance « d » de la Terre fut en réalité émise à l’instant (t – d / 300.000), alors que cet astre occupait une position autre sur la voûte céleste. La différence entre la position apparente et la position réelle de cet astre sera d’autant plus importante que l’objet visé est éloigné. Bradley revint sur les observations de Picard dont les fréquents déplacements lui avaient interdit d’effectuer des observations suivies, mais qui avait cependant noté que sur une durée de dix années, une autre cause inconnue avait souvent changé les résultats, sans rendre pourtant la période méconnaissable. Bradley analysa ces données et les recoupa avec ses propres mesures. Il s’aperçut que cette « complication » qui avait interpellé Picard, évoluait suivant un cycle de dix huit ans (comme celle des nœuds de la Lune). Il devenait clair pour Bradley qu’il était en présence d’une nutation de la Terre sur son axe. Bradley attendit 1748 pour publier ses conclusions. Grace à ces deux découvertes, l’astronomie devenue « moderne » allait pouvoir réaliser des progrès considérables. En 1741, Bradley succède à Halley à l’Observatoire Royal. Le roi lui confie le vicariat de Greenwich, qu’il refuse, tant il craint que cette nouvelle charge ne viennent perturber ses travaux d’astronome. Bradley sera également un des huit associés étrangers de l’Académie des sciences de Paris à partir de 1748. Il obtiendra la médaille Copley (médaille la plus prestigieuse attribuée par la Royal Society). Ce n’est étonnement qu’en 1752 qu’il sera enfin admis au sein de cette académie. En tant qu’un des principaux promoteurs du calendrier Grégorien en Angleterre, il faillit être lapidé par une population de fanatiques opposants. Il mourut à l’âge de soixante-douze ans, au terme de deux années de souffrance et de maladie.
