Alexis Claude Clairaut (1713-1765)
Alexis Claude Clairaut (1713-1765) est né à Paris, second enfant d’une famille très nombreuse, il ne compte pas moins de vingt frères et sœurs ! Son père Jean-Baptiste est professeur de mathématiques, membre des Académies Royales des Sciences de Paris et de Berlin. Alexis Claude est un jeune prodige. Dans son éloge, écrit en 1768 par Jean Baron, secrétaire perpétuel de l’académie d’Amiens, on peut lire: « En apprenant à lire dans Euclide M. Clairaut l'entendit, et n'avait que 5 ans; c'était renouveler et surpasser la merveille de Pascal. Un coup d'œil jeté sur l'énoncé des théorèmes les lui démontrait: la solution des problèmes réservés à ceux qui avaient vieilli dans les mathématiques ne fut qu'un des jeux de son enfance. À 9 ans l'application de l'algèbre à la géométrie lui était familière. À 11 ans il entendait les Sections coniques et l'Analyse des infiniment petits du Marquis de l'Hôpital*, avec lequel il eut plus d'un trait de ressemblance. Au même âge il avait découvert quatre courbes du troisième genre (degré) sur lesquelles il fit un mémoire qui fut imprimé, avec le certificat le plus honorable, dans le recueil de l'Académie de Berlin: car il est bon d'avoir pour cette espèce de prodiges des témoins et plusieurs témoins irréprochables. Quand il commença son excellent et fameux ouvrage sur les courbes à double courbure, il n'avait que 13 ans : on ne peut s'empêcher de marquer toujours exactement des dates si singulières ». Clairaut ne s’arrêtera pas là. A dix huit ans, il publie un livre de géométrie Recherches sur les courbes à double courbure, qui lui vaut son admission à l’Académie des sciences, pour laquelle il fait l’objet d’une dispense exceptionnelle en raison de son jeune âge. Clairaut qui fait partie de l’expédition en Laponie, dirigée par Maupertuis, est également connu pour un théorème qui porte son nom, publié dans Théorie de la figure de la terre tirée des principes de l’hydrostatique, dans lequel il relie la gravité aux points de la surface d’un ellipsoïde en rotation, à la compression et à la force centrifuge à l’équateur. Son théorème servira, entre autre, pour calculer l’aplatissement de la Terre.
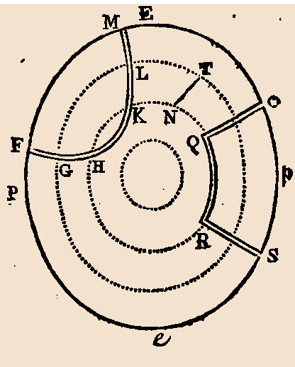A part d’être mathématicien soi même, il est difficile de comprendre ses calculs et ses démonstrations. Sachons qu’il part du principe que sa sphéroïde est hétérogène et qu’il développe sa théorie sur la base de ce postulat. La figure ci-contre qui représente différents aspects de cette sphéroïde qu’il va étudier en atteste (Cette sphéroïde peut être en l’occurrence une planète comme la Terre). J’ai parcouru son ouvrage et j’en restitue ici un extrait qui devrait permettre de comprendre, au moins, certaines de ses hypothèses. L’extrait est issu de l’introduction de la seconde édition de son livre, parue en 1808: « Quand on considère tout ce qui compose la surface de notre globe, les continents, les mers, les lacs, les montagnes, les courants des fleuves, etc.; on est d'abord porté à croire que toutes les recherches que peut fournir la théorie pour déterminer la figure de la terre, sont de vaines spéculations, et que même la mesure actuelle, ne saurait nous en faire connaître que de très petites parties, sans en pouvoir conclure pour le tout. Quand on remarque ensuite que les mers communiquent ensemble de toutes parts, que les côtes ne sont que très-peu élevées au-dessus de la mer, que la hauteur des plus grandes montagnes est presque nulle en comparaison du diamètre de la terre, que la déclivité des plus grands fleuves ne suppose pas que leurs sources soient plus élevées au-dessus du niveau de la mer, que ne le sont les montagnes; on vient bientôt à reconnaître que la figure de la terre doit dépendre des lois de l'hydrostatique, et que les opérations faites pour la mesurer doivent donner à peu près les mêmes résultats que si on les faisait sur une masse d'eau qui se serait durcie après avoir pris la figure que demande l'équilibre. »
Dans son ouvrage, Clairaut réfute la théorie des tourbillons de Descartes et affiche ses préférences pour Newton. Il dit « L’illustre Descartes qui n’avait pas été à portée de connaître des lois que les planètes observent dans leurs mouvements, ne croyait avoir à expliquer dans le phénomène de gravité, que cette tendance que tous les corps ont ici-bas vers le centre de la Terre. Pour en trouver la raison, il supposa que la Terre était enveloppée d’un tourbillon de matière subtile qui circulait sans cesse, et comme cette matière en circulant devait faire un effort pour s’écarter du centre du tourbillon, il prétendit que les corps graves ayant moins de force centrifuge que cette matière, ils cédaient à son effort, et étaient chassés vers le centre de la terre. Depuis M. Newton a paru, les Cartésiens éclairés ont été forcés de reconnaître, que la force de la pesanteur était répandue dans tout l’univers; ils sont enfin convenus que la Lune est un corps grave qui pèse vers la Terre et toutes les planètes ont une semblable gravité vers le Soleil, ainsi que les satellites vers leurs planètes principales, et se trouvant encore obligé d’avouer que toutes ces gravités augmentent dans la même raison que le carré de la distance au corps central diminue ». Il conclut: « La théorie précédente (la sienne), se trouvant donc d’accord avec toutes les mesures du pendule et avec l’observation des diamètres de Jupiter; s’il arrive, outre cela, que les mesures que nous attendons du Pérou comparées à celles qui ont été faites en Laponie, rendent la différence des axes moindre que 1/230ème, cette théorie aura toute la confirmation possible, et la gravitation universelle, qui s’accorde si bien avec les mouvements des planètes, s’accordera encore avec leurs figures ».
En 1765, Clairaut publie également une Théorie de la Lune (ci-contre) dans laquelle il laisse de côté ses travaux sur les sphéroïdes et l’hydrostatique, pour exploiter les seules théories de Newton. Pour cet ouvrage, il reçoit le prix de l’Académie impériale de Saint Petersbourg. Il publiera également une théorie sur les trajectoires des comètes. Clairaut eut également un rôle auprès de la marquise du Chatelet qui travaillait à sa traduction des Principia de Newton.
Maupertuis délaissant sa compagnie, elle se rapprocha alors d’Alexis Claude que lui avait présenté ce dernier et qui devint son nouveau professeur de géométrie, tout en faisant son initiation en astronomie. Il trouva son élève douée, mais ne put pas en dire autant de Voltaire qui, résidant alors dans la demeure de la marquise, se joignait à leurs cours. Pierre Brunet dans sa biographie La vie et l’œuvre de Clairaut, publiée en 1952, reproduit les commentaires de ce dernier: « J’avais là deux élèves de valeurs très inégales, l’une tout à fait remarquable, tandis que je n’ai pu faire entendre à l’autre (Voltaire) ce que sont les mathématiques ».
Dans le « Dictionnaire Universel » de Louis Mailleul Chaudon, publié en 1810, on trouve enfin une partie de l’éloge de Clairaut publiée à sa mort dans le Journal des savants : « M. Clairaut, dit le panégyriste, ne nous a rien donné que d’excellent. Il traitait en maître, et presqu’en se jouant, les objets de son ressort lorsqu’il les jugeait digne de lui; Mais il avait peu le loisir de s’occuper de rendre compte des idées des autres, tandis qu’il avait lui-même tant d’idées importantes à exposer pour le progrès des sciences, tant de découvertes utiles à publier. Souvent, en lisant les ouvrages qu’il se proposait d’analyse, il s’abandonnait à l’ardeur de découvrir, et quittait l’auteur pour résoudre les problèmes. Dans nos assemblées, où il était fort assidu, nous avions eu lieu d’admirer constamment cette modestie, cette douceur, qui doublaient le prix de ses talents. Sur les matières les plus étrangères aux travaux qui remplirent toute sa vie, il avait le goût le plus fin et le tact le plus sûr; s’il critiquait peu, et toujours avec douceur, il applaudissait toujours à propos; et son approbation, dont il n’était ni prodigue ni avare, était en tout genre un prix très flatteur. Clairaut mourut en 1765 dans les bras de son père, qui avait déjà vu périr dix-neuf enfants. »
* Guillaume François Antoine de l’Hôpital (1661-1704) Mathématicien et académicien français, Il est le premier à avoir écrit un traité sur le calcul infinitésimal différentiel «L'Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes » .