James Clerk Maxwell (1831-1879)

James Clerk Maxwell (1831-1879) est né à Édinbourg. Son père, avocat, est issu d’une famille de riches propriétaires terriens. Enfant, il fait preuve d’une curiosité insatiable. Dés qu’il sait parler, il pose des questions à tout propos. Sa mère prend en charge son éducation, comme c’est la coutume dans l’Angleterre victorienne, mais elle meurt lorsque James à huit ans. Son père engage alors un jeune précepteur de seize ans, avec lequel James ne peut travailler correctement car il ne supporte pas la dureté et les railleries incessantes du jeune homme que le père finira par congédier. Aidé par sa belle sœur, il prend alors en charge l’éducation de son fils. Vers l’âge de dix ans, James est envoyé à l’Académie d’Edinburg, il loge chez une tante qui lui apprend le dessin. Comme la classe de première année est complète, on l’inscrit directement en deuxième année. James est le plus jeune de sa classe. Son accent et son allure provinciale lui valent des moqueries et d’être surnommé «idiot ». Durant une année, il reste à l’écart et n’entretient quasiment aucune relation sociale. Heureusement, l’année suivante, il lie une relation amicale avec Lewis Campbell et Peter Guthrie Tait, qui resteront ses amis pour la vie. Lewis Campbell deviendra professeur à Oxford et Peter Guthrie sera un physicien et mathématicien connu pour ses travaux sur l’énergie. Pendant ses premières années d’étude, rien ne distingue James. En revanche, à l’âge de treize ans, il remporte le prix de mathématiques de son école ainsi que les premiers prix d’anglais et de poésie. Deux ans plus tard, il rédige un premier article intitulé « oval curves ». Il y traite de la manière de tracer des courbes mathématiques à l’aide d’un morceau de ficelle, des propriétés de l’ellipse et d’autres courbes à foyers multiples.

Son article est remarqué, mais comme il est trop jeune pour le présenter lui même devant les membres de l’Académie Royale d’Edinburg, c’est John Forbes, l’éminent professeur de mathématiques qui s’en charge. A seize ans, James quitte l’académie pour entrer à l’université. Il a déjà formulé le souhait d’embrasser une carrière scientifique. Rapidement, il trouve que ses professeurs ne sont pas suffisamment exigeants et il décide d’approfondir ses connaissances en autodidacte. Il passe alors tout son temps libre plongé dans des livres de chimie, d’électricité et d’optique et il commence à réaliser ses propres expériences. C’est à cette époque qu’il se passionne pour l’étude de la lumière polarisée. Il utilise des prismes en verre, à travers lesquels il envoie de la lumière vers des blocs de gélatine qu’il modèle pour étudier le comportement des rayons lumineux. Il découvre ainsi la photoélasticité qui permettra de déterminer la distribution des contraintes au sein de structures physiques. Il quitte Edinburg pour Cambridge où il est admis au Trinity Collège. Il obtient son diplôme de mathématiques à vingt trois ans et prolonge alors ses recherches sur les propriétés des couleurs. En 1807, alors que les physiciens étaient encore sous l’influence des sept couleurs élémentaires du prisme de Newton, considérées comme non mélangeable, Thomas Young remarque que seulement trois des couleurs du spectre de la lumière suffisent à reconstituer toutes les autres. Maxwell plonge dans les travaux de Young et pousse plus loin ses investigations. Il rédige un article "Experiments of colors" qu’il présente cette fois lui-même à la Royal Society d’Edinburg. Ci-dessus on le voit en 1855, avec une de ses « toupie de couleurs » à la main. Depuis longtemps les peintres mélangeaient leurs couleurs pour en obtenir de nouvelles. Tobias Mayer avait étudié la question et tenté une approche quantitative, en mesurant précisément les dosages de pigments. Maxwell abordera tout  autrement cette problématique.

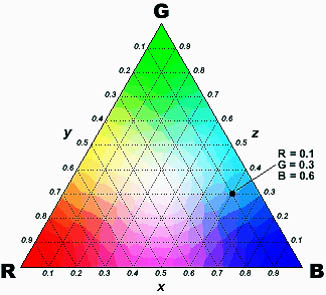Il cherche en effet à définir quantitativement les composantes entrant dans la constitution d’une couleur, en tant que résultante de différents dosages d’autres couleurs. Tandis que son professeur John Forbes s’obstine à obtenir un gris à partie du rouge du jaune et du bleu, Maxwell opte pour les couleurs vert, bleu et rouge. Maxwell remplit les « toupies », inventées par Forbes, avec différentes couleurs puis, il les fait tourner à grande vitesse de telle sorte que l’œil perçoive une couleur résultante. Il découvre que le blanc est  une association des trois couleurs vert bleu et rouge, ce qui lui permet d’en déduire que la lumière blanche résulte d’un mélange de lumières rouges vertes et bleues. Il est alors en mesure de composer un triangle trichromatique (ci-contre) permettant de quantifier les proportions des trois couleurs de base entrant dans la constitution de toutes les autres. En 1855, alors qu’il n’est que fellow au Trinity Collège, il propose sa théorie de la vision colorée, considérée comme à l’origine de l’étude quantitative des couleurs: la colorimétrie. En 1857, il s’intéresse aux anneaux de Saturne et montre que ces derniers sont  probablement constitués d’une multitude de petits corps solides en orbite autour la planète et circulant à des vitesses conformes aux lois de Kepler. En 1860, il reçoit la médaille Rumford pour son travail et, l’année qui suit, il réalise la première photographie en couleur. En 1865, il se retire dans sa propriété écossaise et rédige Traité sur le magnétisme. En 1871, il revient à Cambridge où il est nommé professeur de physique expérimentale. Il développe alors un laboratoire de recherche, le Cavendish Laboratory, grâce à des fonds privés. Ce laboratoire inauguré en 1874, deviendra un des foyers mondiaux de la recherche scientifique. Ci-dessous, une lettre de Maxwell à Lord Kelvin, dont les avis à propos de l’éther divergeaient du sien.

Bien que Maxwell ne soit pas un astronome, les retombées de ses travaux auront d’importantes répercussions en astrophysique. Par exemple, les quatre équations de champ qui portent son nom peuvent expliquer la propagation de la lumière et suggérer l’existence des ondes électromagnétiques que nous utilisons chaque jours avec nos téléviseurs postes de radio ou téléphones. Maxwell montre que les radiations lumineuses doivent être considérées comme des oscillations de champs électriques et magnétiques. Vers 1860, il calcule qu'une onde électromagnétique se propage à une vitesse avoisinant 310.740 km/s. Vitesse qu’il rapproche avec la vitesse de la lumière qu’Hippolyte Fizeau et Jean Foucault avaient mesurée quelques années auparavant, à environ 298.000 km/s. Maxwell tire la conclusion qui s'impose et en déduit que la lumière doit être comme une onde électromagnétique, oscillation simultanée des champs électrique et magnétique qui se propage à une vitesse voisine de 300.000 km/s. Dés lors, on put expliquer comment un rayon de lumière parvenait à traverser le vide et donc, comment la lumière des étoiles arrivait jusqu’à nous, sans que la présence d’un éther emplissant le vide intersidéral soit nécessaire. Cette réunification entre les théories de la lumière et celle de l’électromagnétisme est considérée comme une des plus grandes avancées scientifiques du XIX^ème siècle dans le domaine de la physique. Dans les quatre conférences qu’Albert Einstein donne en 1922 à l’université de Princeton, les références aux équations de Maxwell sont omniprésentes. Einstein avouera d’ailleurs: «La théorie de la relativité doit son origine aux équations de Maxwell sur le champ électromagnétique». Maxwell laisse également un œuvre fondamentale dans son ouvrage Théorie dynamique des gaz. Il y aborde la description statistique des mouvements et leur traitement par les mathématiques. Connue sous le nom de répartition de Maxwell, elle constitue également une des bases de la physique. Toute sa vie, Maxwell sera attaché aux questions religieuses et philosophiques. A quarante huit ans, il meurt prématurément d’un cancer de l’estomac.