Johannes Kepler (1571-1610)

Johannes Kepler (1571-1610) est né à Weil der Stadt dans le Wurtemberg. Arrivé deux mois avant terme, il garde de sa naissance prématurée une constitution délicate. Sa vie personnelle ne sera pas très heureuse, car aussitôt mis au monde, sa mère l’abandonne pour suivre son père alors engagé dans l’armée espagnole durant la guerre d’indépendance des Pays-Bas. Ses grands parents l’élèvent jusqu’au retour, quatre ans plus tard, de ses parents qui le retrouvent en très mauvaise santé, atteint de surcroit par la vérole. Il peut cependant en guérir et rentrer à l’école de Loewenberg où il apprend à lire et à écrire. C’est à cette époque qu’on lui donne le surnom «Léomontanus». Ses parents se sont installés comme aubergistes, mais ils font de mauvaises affaires. Le père de Johannes doit s’engager de nouveau, cette fois dans l’armée autrichienne en guerre contre les Turcs. Kepler a deux frères, l’un fondeur d’étain et l‘autre soldat. Ces derniers, véritables voyous sont pourtant les préférés de leur mère, elle-même dure et irascible. Elle fait souffrir Johannes qui ne trouve quelque réconfort qu’auprès de sa sœur Marguerite, mariée avec un pasteur. Pour aider son jeune beau-frère, ce dernier l’emploie pour divers travaux de manutention, mais sa frêle constitution ne lui permet pas de les assumer durablement. Le pasteur, un peu embarrassé par ce beau-frère chétif, lui offre, probablement pour le tenir à l’écart de son ménage, l’opportunité de rentrer à l’école du cloitre de Maulbronn, où il va également apprendre la musique et s’avérer par ailleurs si brillant, qu’il va pouvoir rejoindre le collège Ducal de Thuringe où il obtiendra le titre de maitre-ès-sciences. Kepler se destine à une carrière ecclésiastique, lorsqu’il a l’idée de suivre les cours d’astronomie prodigués par le successeur de Pierre Apian à la chaire d’astronomie de son collège.

Il nous laisse des traces écrites de cet épisode: «C’est en vérité une voix divine qui appelle les hommes à l’étude de l’astronomie, cette science exprimée, non par des mots et des syllabes mais par le monde lui-même, par cet effort sublime de l’intelligence humaine à se mesurer avec l’ordre des corps célestes… Je ne manquais pas de dispositions naturelles et comprenais assez bien ce qu’on y enseignait de géométrie et d’astronomie dans les écoles. Mais il n’y avait là rien qui pût décider de ma vocation. J’étais élève aux frais du Duc de Wurtemberg; et lorsque je voyais mes camarades hésiter, sur l’invitation de leur prince, à voyager à l’étranger, je résolus d’accepter tout ce qu’il m’offrirait». A vingt trois ans, il est nommé professeur de mathématiques à Gretz où on lui commande de surcroit la rédaction d’un almanach, consécutivement à la réforme du calendrier grégorien. Kepler est fortement influencé par ses études de théologie. Cette emprise apparait clairement dans une description qu’il fait alors de l’Univers «Avant la création du monde, il n’y avait d’autre nombre que la trinité qui est Dieu lui-même. A part les corps irréguliers, il n’y a que six corps réguliers: la sphère et les cinq corps rectilinéaires. Le monde est double, mobile et immobile. Le monde immobile est occupé par les étoiles fixes, le soleil, et l’éther intermédiaire, trois éléments qui correspondent dans la trinité au père, au fils et au saint esprit. Le monde mobile est occupé par les six planètes tournant autour du Soleil qui présente l’image du père créateur: Le Soleil distribue le mouvement comme le père répand le saint esprit.» De ce texte ressort cependant son adhésion au système copernicien. Il publiera par la suite Mysterium cosmographicum,  au sujet duquel Tycho Brahé ne se trompe pas en faisant son éloge. A vingt six ans, Kepler se marie avec une riche héritière qui exigera cependant de lui qu’il présente des titres de noblesse. Ce mariage n’est pas heureux, d’autant que rapidement Kepler doit faire face à la persécution qu’exercent les prêtres catholiques sur les professeurs protestants. Il doit fuir le collège de Gretz, malgré qu’il ait ouvertement critiqué ses coreligionnaires qui refusaient de se soumettre à l’autorité du pape Clément VIII (le même qui a fait condamner Giordano Bruno au bûcher). Il est, dans sa fuite, obligé de vendre ou de louer une grande partie des biens de son épouse, avec laquelle il a trois enfants qu’il va perdre en 1611, en même temps que leur mère, devenue épileptique puis folle. C’est alors que Tycho Brahé l’invite à Prague, pour l’aider à achever ses travaux. Il s’y rend avec enthousiasme, mais une fois de plus il va trouver une situation qu’il n’avait pas soupçonnée, tel qu’en témoigne cet extrait d’une lettre qu’il envoie à un de ses amis: «Tout est incertain, Tycho est un homme dur et hautain, avec lequel il est impossible de vivre…».  Kepler est mal rémunéré et sa situation n’est guère enviable, jusqu’à ce que la mort de Brahé vienne le libérer et lui permettre d’être nommé astronome de l’empereur Rodolphe II. Il s’établit alors à Lintz à proximité de Vienne.

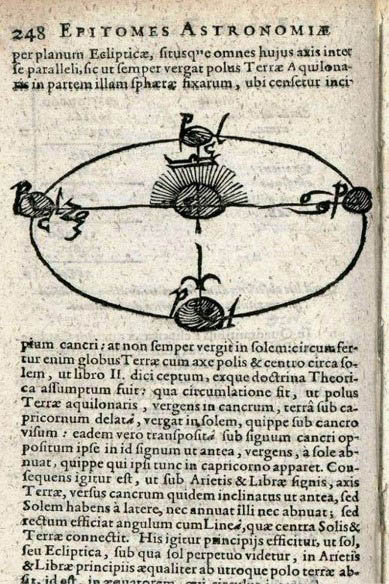A la mort de l’empereur, son successeur Matthias I^er, reconduit Kepler à son poste et lui confie le soin de corriger le calendrier grégorien. Mais Kepler ne parvient pas à se faire payer pour son travail et doit pour survivre publier divers almanachs. Il en est réduit à tirer les horoscopes pour des princes désireux de connaitre leur avenir. Kepler se console de ses déboires en consultant les manuscrits de Tycho, auxquels il a un libre accès. Ses mésaventures ne sont pas finies, sa propre mère accusée de s’adonner à la magie, aurait été initiée par une tante, brulée vive pour sorcellerie. Kepler arrive à la sauver in extrémis, mais de retour à Linz, il doit affronter les accusations des prêtres catholiques qui lui reprochent d’être le fils d’une sorcière. Kepler se remarie, mais ses faibles revenus ne suffisent pas à subvenir aux besoins d’un ménage de sept enfants. Il se bat encore pour faire valoir ses droits et l’argent qu’on lui doit, mais en vain, car l’empereur Ferdinand II, qui succède à Matthias I^er hérite aussi d’une importante dette. Physiquement éprouvé et moralement anéanti, Kepler meurt à l’âge de cinquante neuf ans. La vie de cet homme est parsemée de moments noirs, en revanche il n’a jamais cessé de travailler. Il rédige entre autres, Astronomia nova qui à lui seul suffit à le placer parmi les plus grands astronomes. Il est le premier à avoir osé s’opposer au dogme établi de la perfection des mouvements célestes, considérés depuis l’Antiquité comme parfaitement circulaires et que, ni Galilée, ni Copernic ne remirent en cause. On peut se poser bien des questions sur ce qui conduisit Kepler à envisager des trajectoires elliptiques pour les planètes, justifiant par exemple, le fait déjà évoqué que les astres mobiles ont une luminosité variable. En effet, il fait référence aux «mouvements révolutifs des corps célestes uniformes et circulaires» et les décrit comme ayant été seulement «admis». Les lieux considérés pour la position des astres étaient alors des lieux dits «moyens», approximation commode pour les calculs de positions, mais qui en réalité ne coïncidait pas parfaitement avec les positions réellement observées des astres. Insatisfait de cet état de choses, Kepler va alors se lancer dans une description de «l’apparent et du réel» de «l’accessoire et du principal», qui vont lui permettre d’aboutir à la conclusion que: «Les lieux vrais, sont les seuls à pouvoir concilier l’observation et le calcul»,  éliminant ainsi les «lieux moyens» communément admis.

On peut noter que dans un de ses ouvrages, Kepler fait un parallèle surprenant entre l’astronomie et la musique, qu’il a étudiée dans sa jeunesse. Non sans rappeler la démarche de Pythagore, il évoque des similitudes entre les notes montantes et descendantes de la gamme et leur correspondance avec les variations de la course de planètes. Il est difficile de croire cependant que la seule harmonie musicale le mit sur la voie de ses découvertes. En réalité, Kepler est surtout un mathématicien travaillant à démontrer l’existence de lois mathématiques qui régiraient la course des astres. Il est ainsi le premier à faire correspondre les équations avec les positions réelles des astres. Désormais vérifiables par l’observation, elles vont devenir la base d’une astronomie nouvelle ou l’approximation n’aura que très peu de place. Kepler énonce des lois qui prouvent sans équivoque que les anciens, depuis Aristote ainsi que les plus grands astronomes avant lui, se sont trompés. Il travaille également dans le domaine de l’optique et cherche à définir la nature de la lumière en étudiant son comportement à travers des lentilles, sur les miroirs et dans les chambres obscures.

Les deux schémas ci-dessous illustrent les lois de Kepler. L’application de ces seules lois permettra à un mathématicien astronome, Urbain le Verrier, deux cent trente sept ans plus tard de découvrir la planète Neptune. Montrant par là même la formidable puissance de l’outil mathématique.
Dans la première loi (schéma ci-contre), Kepler dit : « l’orbite des planètes décrit une trajectoire elliptique dont le Soleil occupe un des deux foyers » (ici, f1).
La somme des distances (f1, P ) + (f2, P), égale à la distance (A, B) (grand axe de l’ellipse) est constante. On peut le vérifier en traçant une autre position de  P,  qu’on nommera  P’  et en relevant que la somme des valeurs de (f1, P’) +( f2, P’) qui sera identique à la valeur de la distance séparant A à B.
Cette première loi, publiée en 1609 dans Astronomia nova, découle de l’utilisation par Kepler des relevés que Tycho Brahé a effectués pour la planète Mars. Dans le système héliocentrique, le Soleil occupe un des deux foyers f1 ou f2 de la trajectoire des planètes qui gravitent autour de lui.

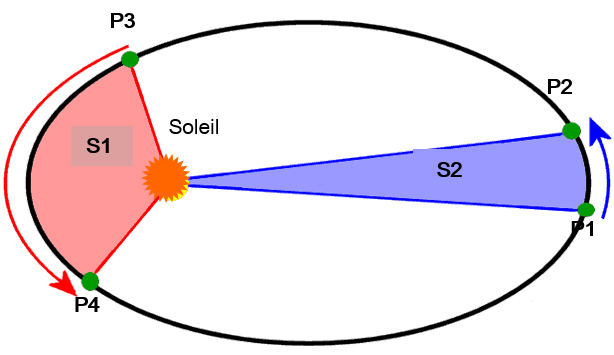Dans sa deuxième loi (schéma ci-contre) Kepler énonce: «Le rayon vecteur reliant le Soleil à une planète balaie des aires égales en des périodes égales». Ce qui signifie qu’une planète (points verts) mettra le même temps pour parcourir la distance définie par la flèche bleue (P1, P2) que celle définie par la flèche rouge (P3,P4), induisant une variation de la vitesse angulaire. Kepler le démontre, en montrant que les surfaces S1 et S2 ont la même valeur.

Il établit, en 1618, une troisième loi qui montre que le rapport entre le cube du demi grand axe (figure ci-dessus) de l’orbite et le carré de la durée d’une période de révolution est constant pour tout système planétaire gravitant autour d’un objet central. Ainsi, le demi grand axe étant = D/2 et, si on appelle «  t » la période que met une planète en orbite autour du Soleil pour effectuer une révolution complète, Kepler montre que: (D/2)³ =  t² = constante.
Comme on l’a évoqué, Kepler fut l’inspirateur de Newton. On peut s’en convaincre en lisant ce qu’il écrit au sujet de la gravitation: «Toute matière resterait au repos, si elle était absolument isolée et en dehors de la sphère de vertu (sphère d’influence) d’un autre corps. La pesanteur tient à la matière, elle est d’une action réciproque entre les corps de même espèce, qui les porte à se réunir, comme on l’observe dans l’aimant, de telle sorte que la Terre attire beaucoup plus une pierre qu’une pierre n’attire la Terre…»

Il continue en évoquant les marées dont il avait compris la cause: «Si la Terre cessait d’attirer les eaux, tout l’océan s’élèverait vers la Lune pour faire corps avec elle. La sphère d’attraction de la Lune s’étend jusqu’à la Terre, et entraine les eaux vers la zone torride (partie du globe entre les deux tropiques comprenant l’équateur) en sorte qu’elle vienne à la rencontre de la Lune dans tous les points ou la Lune est au zénith». Enfin, Kepler a également été un précurseur, lorsqu’il décrivit l’air, considéré alors comme sans masse: «Je n’ignore pas, croyez le bien, qu’en soutenant que l’air a toujours été pesant, je vais encourir le blâme des physiciens mais la contemplation de la nature entière me confirme dans mon idée». Torricelli ne découvrira la pesanteur de l’air que quarante ans plus tard.