Arthur Stanley Eddington (1882-1944)

Arthur Stanley Eddington (1882-1944) est né à Kendal, dans le nord-ouest de l’Angleterre. Il est issu d’une famille de Quakers. Son père est directeur de l’école Stamongate School de Kendal, lorsqu’il est victime d’une épidémie de typhoïde. Sa mère, Sarah Ann Shout, doit alors se satisfaire de faibles revenus pour élever Arthur qui n’a que deux ans, ainsi que sa sœur ainée. La famille déménage à Weston-super-Mare, où Sarah Ann s’occupe personnellement de l’éducation d’Arthur, avant de l’inscrire pour trois années à l’école préparatoire. A l’âge de onze ans, il entre à l’école primaire Brymelin School en tant qu’externe, alors que la majorité de ses camarades sont inscrits en pensionnat. L’école dispense un enseignement de qualité qui permet à Arthur de révéler ses talents en mathématique et en littérature anglaise. Rapidement pourtant, Arthur touche les limites que peut lui offrir cette école en mathématiques et il est contraint de stopper sa progression, en atteignant les équations différentielles et le calcul intégral. Le comté de Somerset récompense sa scolarité par une bourse de soixante livres pour une durée de trois ans, qui doit lui permettre de financer son entrée à l’université. Arthur qui n’a pas encore atteint l’âge minimum de seize ans, obtient une dérogation et s’inscrit au Owens Collège de Manchester. Pour sa première année, il suit des cours dans les matières générales, mais à partir de la seconde année, il se consacre essentiellement à l’étude de la physique. Il subit l’influence d’un de ses professeurs de mathématique, Horace Lamb, qui sera l’auteur d’ouvrages de référence en physique et deviendra membre de la Royal Society, ainsi que lauréat de la médaille Royale et de la médaille Copley. La mère d’Arthur ne peut l’aider financièrement. Ce dernier participe donc aux nombreux concours proposées aux élèves et parvient à subvenir à ses besoins, grâce aux récompenses substantielles qu’il parvient à obtenir.

Vers la fin de 1901, il décroche une bourse de soixante quinze livres qui lui permet d’entrer au Trinity Collège de Cambridge. L’année suivante, le montant de cette bourse est porté à cent dix livres. Il se consacre alors entièrement à l’étude des mathématiques. Il est pris en main par trois professeurs prestigieux: Edmond Taylor Whittaker (médaille Copley), Alfred North Whitehead (médaille Sylvester) et Ernest William Barnes de la Royal Society. En 1904, Arthur devient Senior Wrangler en mathématiques, distinction qui caractérise l’étudiant qui a obtenu les meilleurs résultats en troisième année d’étude. L’année suivante, il obtient son diplôme de deuxième cycle. Il entre, dans un premier temps, au Cavendish Laboratory où il travaille sur les émissions thermoïoniques. Il entreprend également des recherches en mathématiques, mais il ne poursuit dans aucune de ces deux voies. Un peu avant la fin 1905, il entre dans le domaine de l’astronomie, en rejoignant un poste à l’observatoire royal de Greenwich. Sa seule expérience datait de son enfance, où il avait été intrigué en observant le ciel à l’aide d’une petite lunette qu’on lui avait prêtée. Sa première tâche consiste à étudier des plaques photographiques réalisées pour l’astéroïde 433 Eros, sur une période d’une année, afin de déterminer avec précision la valeur de la parallaxe solaire. A cette occasion, il développe une nouvelle méthode statistique qui prend en compte la dérive apparente de deux étoiles en fond de ciel. Pour ce premier travail, il reçoit le Smith’s Prize de l’université de Cambridge en 1907. En 1912, alors qu’il occupe une chaire d’astronomie et de physique expérimentale à Cambridge, Sir Georges Howard Darwin, le second fils de Charles Darwin, meurt. Eddington est appelé pour le remplacer. Peu de temps après Sir Robert Stawell Ball, qui occupait la chaire d’astronomie et physique théorique décède à son tour. Eddington est alors nommé directeur de l’observatoire de Cambridge qui intègre la totalité des disciplines astronomiques théoriques et expérimentales. Il est élu Fellow de la Royal Society . En 1914, le première guerre mondiale éclate. Eddington, appelé pour son service militaire ne veut pas combattre. En tant que quaker, il est résolument pacifiste et objecteur de conscience. Il demande à être affecté dans un service d’intérêt général, mais cette possibilité n’existe pas. Il obtient pourtant un sursis, grâce à l’intervention d’un de ses collègues, l’astronome royal Franck Watson Dyson, qui plaide en sa faveur, argumentant que la Grande Bretagne ne peut se permettre de perdre un de ses scientifiques les plus renommés. Il est probable que plusieurs facteurs soient intervenus dans cette décision. En premier lieu, en raison de l’importance de la compétition qui existait à l’époque entre différents états, dont la grandeur dépendait en partie des avancées scientifiques et, en second lieu, du fait que la mort récente d’un autre scientifique britannique tué récemment au front était encore, dans les esprits, considéré comme une trop lourde perte.

En 1915, la Royal Astronomical Society diffuse des articles de Willem de Sitter et d’Albert Einstein sur la relativité, dans lesquels ce dernier explique un phénomène, alors sans réponse, relatif à l’avance du périhélie de Mercure. Si ses équations de la relativité générale sont exactes, la déviation de la trajectoire de la lumière à proximité du Soleil est deux fois plus grande que celle que donneraient les lois de la gravitation de Newton. Ce résultat intrigue Eddington qui étudie alors les étoiles variables céphéides. En reprenant notamment des travaux de Karl Schwarzschild, il découvre la relation qui existe entre la masse et la luminosité d’une étoile et il fixe même la luminosité qu’une étoile ne peut dépasser, appelée « limite d’Eddington ». Il calcule la proportion d’hydrogène d’une étoile céphéide et parvient à élaborer une théorie justifiant sa pulsation. En 1926, il publie une synthèse de ses recherches: The Internal Constitution of Stars (La constitution interne des étoiles).

Dans son manuscrit de 1915, Einstein proposait de tester la déviation d’un rayon lumineux passant dans le champ gravitationnelle d’un astre massif, en l’occurrence, le Soleil. A la fin de la guerre, Eddington souhaite profiter de l’éclipse solaire prévue le 29 mai 1919 pour mesurer le déplacement apparent d’étoiles du fond de ciel voisines du Soleil et comparer les résultats avec ceux mesurés sur ces étoiles, lorsqu’elle ne se trouvent pas en incidente rasante. Eddington organise deux expéditions vers des lieux de la Terre où l’éclipse sera totale. Une base est installée à Sobral au Brésil et l’autre sur l’île de Principe, dans le Golfe de Guinée. Les étoiles retenues pour effectuer les mesures seront visibles lors de l’éclipse, elles font partie de l’amas des Hyades situé dans la constellation du Taureau. Si la théorie de la relativité est exacte, les mesures doivent montrer l’image apparente de chaque étoile décalée suivant un déplacement radial autour du Soleil. Les calculs issus des équations d’Einstein, donnent un décalage de 1,75’’ d’arc en moyenne. En effet, plus l’image de l’étoile est proche du Soleil, plus la déviation est importante. Il convient donc de tirer deux séries de plaques photographiques contenant l’ensemble des étoiles autour du Soleil, avant et après l’éclipse et en conservant rigoureusement la même position de visée. Ensuite, la superposition des deux plaques devrait révéler les déplacements.

Le campement et le matériel sont installés (image ci-dessus), à Sobral, le télescope solaire de la Royal Irish Society, déplacé pour l’occasion). Le jour de l’éclipse, la météo n’est pas favorable. Heureusement une belle éclaircie permet à F.W. Dyson, qui dirige la base, de prendre de bons clichés. De l’autre côté de l’Atlantique, la base de Principe ne bénéficie pas d’une météo aussi clémente et Eddington qui observe l’éclipse depuis cette base doit se contenter de clichés pris en partie à travers des nuages. Seules deux de ses plaques seront exploitables. Il séjourne encore quelque temps sur l’ile et réalise les plaques de référence. De retour, il entreprend les analyses. Ses résultats doivent trancher entre trois options. Soit la déviation est nulle, soit elle est voisine de 0,87’’ d’arc (déviation Newtonienne), soit elle est voisine de 1,745‘’ d’arc (déviation einsteinienne). Eddington prend particulièrement en compte deux des étoiles qui apparaissent les plus rapprochées du limbe solaire pour bénéficier, théoriquement, d’une déviation maximale. Mais une multitude d’autres paramètres interviennent dans la précision des mesures, comme la qualité de la mise au point, celle des optiques des instruments, les turbulences atmosphériques, la taille du disque de diffraction (disque d’Airy) sur les plaques photographiques, le nombre d’étoiles observées, leur distribution autour du Soleil et, enfin, l’effet de la réfraction de la couronne solaire pour les étoiles les plus proches. Ci-contre, détail d’une plaque photographique faisant apparaitre, entre les traits rouges, la position que devrait occuper l’étoile de référence, en l’absence de l’influence gravitationnelle du Soleil. Entre les traits verts, on peut distinguer la position de cette même étoile, lorsque sa lumière passe à proximité de la masse solaire.

Compte tenu de tous ces critères, les plaques sont longuement analysées et les premiers résultats tombent: 1,98 ’’d’arc +/- 0,12’’ pour la mesure de Sobral et 1,61’’ d’arc  +/- 0,30 ‘’ pour celle de Principe, très proches de la valeur théorique d’Einstein. Le 6 novembre 1919, à l’occasion d’une réunion de la Royal society, Dyson annonce, sous le portrait de Isaac Newton qui domine cette assemblée, que l’effet Einstein a pu être observé avec succès. Aussitôt, les médias se font l’écho de cette évènement qui hissa Einstein à un niveau de popularité jamais atteint par un scientifique auprès du grand public. La notoriété d’Eddington est également à son apogée; ci-contre, une page entière du London News relate l’expérience. En revanche, un vent de panique souffle sur une partie de la communauté des physiciens, déstabilisée par les conséquences de cette véritable révolution. En effet, désormais ils doivent assimiler le calcul tensoriel et ses équations complexes truffées d’indices, auxquelles, par ailleurs, la seule intuition ne permet plus d’accéder. Certains d’entre eux, qui ne purent jamais s’adapter prirent le parti désespéré de combattre la relativité en tentant d’en minimiser l’impact. Les avis furent quelque temps partagés. Narquois, Arthur Milne, qui cultivait quelques divergences scientifiques avec Eddington lança un jour à ce dernier « Vous devez être l’un des trois hommes au monde qui comprenne vraiment la théorie de la relativité générale d’Einstein », un silence suivit ... Milne ajouta : « Ne soyez donc pas modeste Eddington ». Sortant de son mutisme, Eddington répliqua: « Au contraire, je cherche qui peut bien être ce troisième homme ! ». Vers 1920, revenant sur ses travaux concernant les étoiles, Eddington émet (à juste titre) l’hypothèse que la source d’énergie qui alimente les étoiles provient de la fusion nucléaire de l’hydrogène en hélium. Jusqu’à sa disparition, Eddington consacrera l’essentiel de son temps à tenter une réunification de la théorie quantique de la théorie relativité et de la gravitation. Ci-dessous, on le voit en pleine en conversation avec Einstein. Eddington, s’appuyant sur l’analyse numérologique parviendra à des conclusions pour le moins hasardeuses. Il tenta d’établir des rapports entre les constantes fondamentales (grandeurs fixes ne possédant aucune dimension, que l’on retrouve dans les équations de la physique, et dont la valeur ne peut pas être déterminée par la théorie).

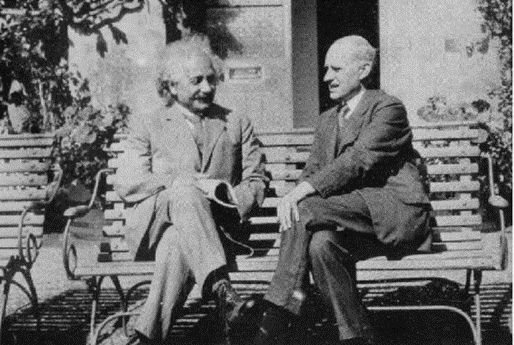Il alla même jusqu’à exploiter des considérations esthétiques pour parvenir à calculer le nombre qui porte son nom et qui est sensé déterminer la quantité précise d’électrons dans l’Univers. En 1938, Il déclare: « Je crois qu’il y a exactement, 15 747 724 136 275 002 577 605 653 961 181 555 468 044 717 914 527 116 709 366 231 425 076 185 631 031 296 protons dans l’Univers et autant d’électrons ».
Eddington donna de nombreuses conférences, au cours desquelles il défendait une cosmologie justifiée par la théorie de la relativité, tout en lui donnant également une dimension philosophique et religieuse. Plus prudent que certains de ses collègues, il n’alla cependant pas jusqu’à tenter une explication scientifique de l’existence de Dieu. Il meurt à l’âge de soixante-deux ans, couvert de distinctions et de titres prestigieux: médaille Bruce, médaille Draper, membre de la Royal Astronomical Society et de la Royal Society. Il est anobli en 1930, reçoit l’Ordre du Mérite en 1938 et fut également président de l’Union Astronomique Internationale, de la Royal Astronomical Society et de la Physical Society.