Temps et espace

Si on ne prend pas de précaution particulière, il parait logique à première vue, que le temps se soit écoulé régulièrement depuis l’origine de l’Univers et qu’il continuera de s’écouler inexorablement à la même vitesse dans le futur. Regardons y de plus prés: Une horloge est un instrument qui permet de mesurer cette valeur immuable en unités données: secondes, heures, jours, ans  etc... Ce concept est bien pratique, mais il se trouve que dés le XIX^ème siècle, des mathématiciens ont commencé à envisager le temps d’une autre manière, parmi eux citons, Lorenz, Planck, Poincaré, Einstein.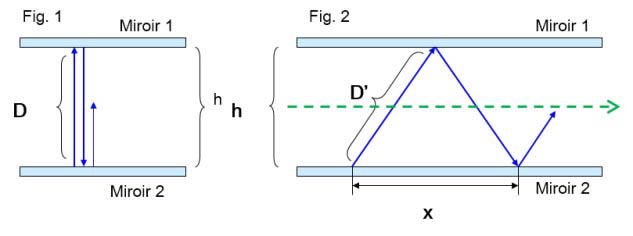  

En effet si l’horloge qui mesure le temps est fixe (fig.1), il apparaît que la valeur de ce temps n’est pas la même que si l’horloge se déplace (fig.2). Dés lors, à partir du moment ou nous mesurons le temps depuis la terre qui n’est pas immobile dans l’univers, quelques savants ont pensé que la valeur du temps mesurée par les horloges terrestres, même si elle nous apparaissait comme une valeur constante depuis la Terre, en réalité ne l’était pas dès lors qu’on changeait de système de référence, par exemple, si on se situait comme un observateur quelque part sur un point très éloigné de la Terre.
Pour mieux comprendre, on se réfère au schéma (ci-dessus) qui illustre ce phénomène: Einstein a imaginé une horloge dont la cadence serait calée, non plus sur un mécanisme quelconque, mais plutôt sur le trajet d’un rayon de lumière (flèches bleues), réfléchi par deux miroirs situés en vis-à-vis (fig1). Le battement de cette horloge virtuelle serait égal à D qui est la durée du trajet de la lumière d’un miroir jusqu’à l’autre. Einstein nous montre comment, si l’on met ce montage en mouvement (fig.2) et qu’on déplace l’horloge d’une distance x, en continuant de mesurer le temps écoulé, on va constater que la lumière aura parcouru la distance D’ pour aller d’un miroir vers l’autre. Hors on constate que la longueur de D’ est supérieur à D, ce qui revient à dire ( comme la vitesse de la lumière est une valeur constante) que lorsque l’horloge se déplace, le temps devient plus long que lorsque l’horloge reste fixe. Cette découverte révolutionna totalement la physique et la mécanique céleste, les équations de Newton devenaient incomplètes et la vision de l’univers s’en trouva totalement bouleversée.
Comme on vient de le voir, l’espace-temps, selon Einstein est différent de celui de Newton. Sa structure est révélée par les trajectoires de la lumière. Dans ce système, tout est repéré par quatre dimensions indissociables: trois d’espace + une de temps. Einstein montre que, de même que transportée dans des endroits différents, une règle n’aura pas la même longueur, le temps est également relatif. Chaque endroit a donc sa propre horloge qui indique son temps à lui seul. Selon le principe de la relativité générale: « tout corps déforme l’espace-temps qui l’entoure ». Cette déformation de l’espace-temps pas perceptible près de la Terre qui n’est pas assez massive, est en revanche observable et mesurable pour le Soleil.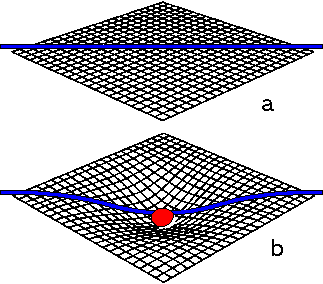

La relativité générale montre que la gravitation n'est pas une force, mais une propriété géométrique de l'espace-temps. En effet, celui-ci est courbé par la masse et l'énergie (traduit par  E=mc²). Ceci peut être résumé par la formule suivante: « L'espace-temps agit sur la matière et lui indique comment elle doit se déplacer. Réciproquement, la matière agit sur l'espace-temps et lui indique comment il doit se courber ». La conséquence est que le temps et l'espace perdent totalement leur caractère absolu, puisque ces deux grandeurs dépendent maintenant de l'endroit où l’on se trouve, d'où le nom de relativité. Bien sur, il est impossible de s'imaginer un espace-temps courbé à quatre dimensions, mais on peut par exemple le représenter en deux dimensions (voir ci-contre). En l'absence de masse (fig.a), l'espace-temps est plat (espace-temps de Minkowski) et la trajectoire de la lumière (trait bleu) est rectiligne. Lorsqu'une masse est présente (point rouge sur la fig.b), l'espace se courbe. Il en va de même pour la trajectoire des rayons lumineux.

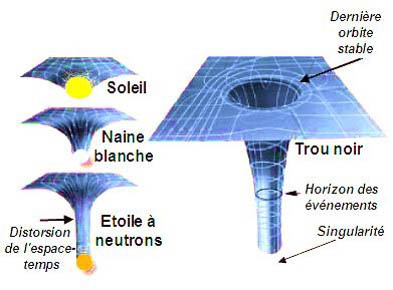Pour élaborer quantitativement sa théorie, Einstein a utilisé des outils mathématiques très complexes, en effet, lorsqu'on parle d'espace courbe, la géométrie dans le plan ou géométrie euclidienne où la somme des angles d’un triangle est égale à 180°, (fig.3 ci-dessous) ne s'applique plus. On doit avoir recours à une nouvelle géométrie développée par Riemann au XIX^ème siècle. Dans celle-ci, la courbure W peut être négative comme la surface d'une selle de cheval (fig.2 ci-dessous), avec une somme des angles d'un triangle inférieure à 180°. Cette courbure peut être aussi positive, c’est le cas à la surface d'une sphère (fig.1 ci-dessous) où la somme des angles du triangle vaut cette fois plus de 180°.
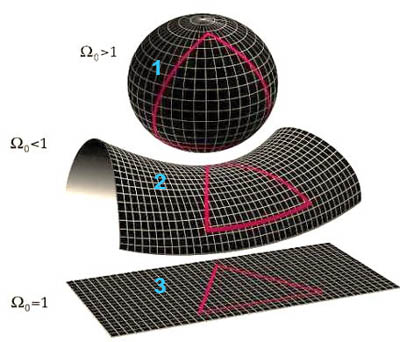La théorie de courbure de l’espace temps est utile en astronomie. Sur le croquis ci-dessus, on peut se faire une idée des interactions suivant les types d’objets. Un trou noir ne peut être envisagé qu'à partir du moment où on se place dans le cadre de la théorie d'Einstein, où l'univers est un espace temps à quatre dimensions, courbé par la gravitation. Le trou noir, de par sa densité extraordinaire, viendra littéralement trouer l'espace-temps en un point. Il y crée une dépression infinie en son centre, nommée singularité. Cela signifie qu'à l'approche de l'horizon d'un trou noir, le temps s'écoule de moins en moins vite et tend à s’arrêter dès que la vitesse de libération atteint celle de la lumière (c’est justement le cas à l'approche de l'horizon du trou noir). Aucune information ne peut nous parvenir d’au-delà de cet horizon, ensuite, c'est toujours le mystère absolu…

NB: A propos de temps, je recommande vivement la lecture du livre de Peter Gallison: "l'Empire du temps" ( Les horloges d'Einstein et les cartes de Poincaré) - Disponible en format de poche: Collection Folio essais (n° 476), Gallimard. Un livre absolument passionnant.