La parallaxe

Pour comprendre simplement comment fonctionne la parallaxe, il suffit de faire l’expérience qui consiste à tendre le bras en levant le pouce devant un objet et de regarder ce dernier successivement en fermant un œil puis l’autre. On constate alors que l’objet situé en arrière plan semble ne pas avoir la même position par rapport à notre pouce, selon qu’on le regarde avec l’œil droit ou avec l’œil gauche.

Ce phénomène dépend de plusieurs facteurs, en premier lieu, de la distance de notre pouce à nos yeux, puis de la distance à laquelle se trouve l’objet visé et enfin de la distance qui sépare notre œil droit de notre œil gauche. 
Si on connait deux de ces trois distances, on peut, grâce à de simples calculs en déduire la troisième. C’est précisément ce phénomène connu des Grecs qui servit aux premières expériences de mesure de distance de la Terre aux étoiles. 

La parallaxe, comme un moyen de mesure des grandes distances, fut utilisée depuis Thales au V^ème siècle avant notre ère pour mesurer des distances terrestres. C’est Jean Dominique Cassini, qui le premier a évalué avec cette méthode la distance d’une planète (Mars) à la Terre. Le schéma ci-dessous, en reprend le principe. A et B représentent deux observateurs situés sur un même méridien, à des latitudes différentes. Pour chacun de ces observateurs, l’angle que fait la direction du Pôle P et l’étoile E est le même: b = b ‘, en effet, dans le cas des étoiles, leurs distances à la Terre gigantesques permettent d’admettre que l’effet de parallaxe est négligeable, avec pour conséquence que AE et BE qui sont assimilables à des parallèles, ne permettent donc pas de mesurer un quelconque écart angulaire. Si maintenant, on effectue la même mesure avec une planète, beaucoup plus proche qu’une étoile, on peut supposer que les écarts angulaires ne seront plus négligeables, bien que très faibles, à supposer également que les instruments disponibles à la fin du XVII^ème siècle soient assez précis. La valeur de l’angle que fera la planète avec une direction de référence va donc varier suivant les points d’observation. C’est cette écart angulaire qui se nomme l’effet parallactique. En réalité, les astronomes ne pourront  mesurer par ce procédé que la distance de la Terre à Mars et à Vénus, les autres planètes étant déjà trop éloignées pour pouvoir obtenir un écart angulaire significatif.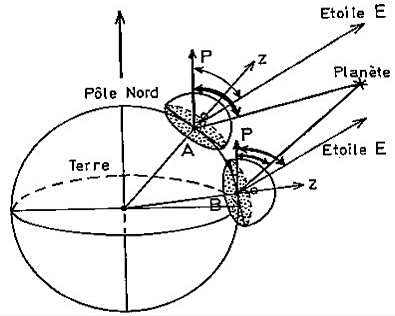

Heureusement les lois de Kepler donnent à ces mesures un champ d’application beaucoup plus vaste. Grâce à sa première loi qui énonce que les orbites des planètes sont des ellipses, on sait que les distances Terre-Vénus et Terre-Soleil vont varier au cours du temps, selon la position des planètes sur leur orbite.

Grâce à la deuxième loi, on sait aussi que les planètes vont plus vite sur leur orbite quand elles sont près du Soleil, ce qui servira à connaître la vitesse angulaire apparente de Vénus (mesurable par exemple lors d’un transit solaire). Enfin, la troisième loi nous permet de connaitre le rapport entre les distances au Soleil de toutes les planètes de telle sorte qu’en connaissant une seule distance dans le système solaire, on saura trouver toutes les autres.
Sur le schéma ci-dessous, on peut voir que la valeur du demi axe de l’ellipse aT varie au cours du temps. Sa valeur rT (à un instant donné), est donnée par la formule:  rT= aT(1-e.cos E) , où (e) est l’excentricité de l’orbite et (E) la variable nommée « anomalie excentrique » qui caractérise l’emplacement de la planète sur son orbite. Inutile d’insister sur le fait que les calculs permettant de traiter ces données sont très fastidieux. Les astronomes employaient donc un personnel de  calculateurs dont la seule tâche consistait à effectuer ces opérations et qui souvent n’entendaient rien à l’astronomie.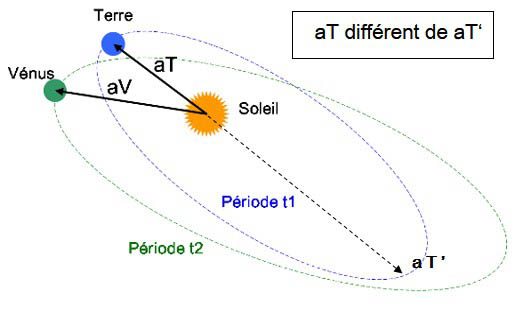

Aujourd’hui la parallaxe est applicable aux étoiles. Mais les valeurs angulaires mesurées dans ce cas sont toujours très faibles. Par exemple la plus grande parallaxe sur une étoile est mesurée avec Alpha du Centaure, étoile la plus proche de nous à une distante de 4.3 al, elle ne fait que 0,76 secondes. Compte tenu des distances, seulement quelques centièmes de secondes angulaires d’erreur correspondent à une approximation de 20% sur la distance.
Cependant ces mesures effectuées par le satellite européen Hipparcos ont permis de répertorier plus de 180.000 étoiles avec une précision voisine de 0.002 ’’. Il existe enfin de nombreuses variantes à la mesure parallactique trigonométrique, par exemple la parallaxe des points de convergence, utilisées sur des amas stellaires comme les Pléiades. Citons aussi les parallaxes spectroscopiques, photométriques, dynamiques, séculaires et surtout la parallaxe annuelle dont la particularité est illustrée dans une mesure à 6 mois d'intervalle sur le schéma ci-dessous.

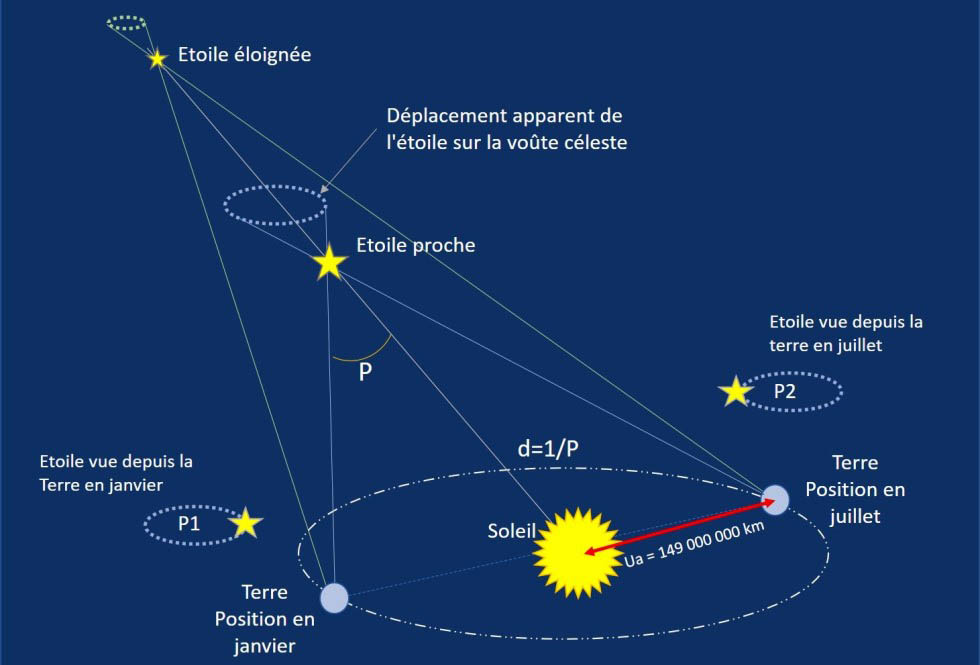
Cette figure  montre comment la révolution annuelle de la Terre sur son orbite, fait apparaitre la trajectoire d’une étoile comme décrivant une ellipse sur fond de voute céleste fixe dans son ensemble. L’expérimentation de cette méthode a permis d’en fixer les limites. On sait aujourd’hui que la mesure des distances d’étoiles situées au-delà de 200 années lumière n’est plus possible en raison de la petitesse des angles mesurés. En fait, l’ellipse de la parallaxe n’est autre que la projection du mouvement annuel de la Terre. La mesure de l’angle de la parallaxe doit être effectué à six mois d’intervalle comme le montre les deux petits schémas (P1) et (P2).