Magnitude
Lorsqu’on observe les étoiles, elles ne brillent pas toutes avec la même intensité. Dès le IIème siècle après J.-C. le grec Hipparque établit un classement des étoiles d’après leur éclat apparent et selon une échelle comprenant six grandeurs. Il positionne l’étoile la plus brillante en 1ère grandeur et ainsi de suite jusqu’à la 6ème qui représente la limite de la vision humaine; c’est ainsi que naquit la magnitude apparente ou visuelle (abréviation: « m » précédant la valeur).
En 1856, l’astronome Norman Pogson établit une formule mathématique caractérisant les magnitudes de -26.8 à +30, il remarque en effet qu'une différence de magnitude dans le système d’Hipparque correspond, en intensité lumineuse (flux), à un rapport donné*. En d'autres termes, l'échelle est logarithmique. L'explication vient du fait que la sensibilité de l'œil à la lumière est elle aussi logarithmique. Ainsi, l'échelle des magnitudes n'est autre que la transcription mathématique de la perception de l'œil. Pogson introduit des valeurs négatives afin de pouvoir classer des objets plus brillants que les « premières grandeurs » d’Hipparque. C’est le cas par exemple pour le Soleil -26.8, la Lune -9, Venus-4.4, Mars -2.8 Jupiter-2.5.
* On constate que le rapport en question est de 100 pour une différence de 5 magnitudes adjacentes. C’est-à-dire que le rapport d’éclat entre deux magnitudes adjacentes correspond à la racine cinquième de 100, soit 2,512... Ce rapport se retrouve dans la relation de Pogson (dans laquelle m est la magnitude apparente et E est la luminosité, pour les étoiles 1 et 2): m1-m2 = -2,5 log (E1/E2) dont le -2,5 correspond au 5 d’écart de magnitude divisé par le logarithme d’un centième (-2) c’est-à-dire 5/-2 = -2,5.
NB: Cette formule de Pogson est à l’origine du module de distance qui est l’outil principal d’estimation des distances en astrophysique puisqu’elle exploite la différence entre la Magnitude absolue d’un objet (que l’on connaît par l’analyse de son spectre) et sa magnitude apparente pour en conclure sa distance: Distance (parsecs) = 10((m-M+5)/5)
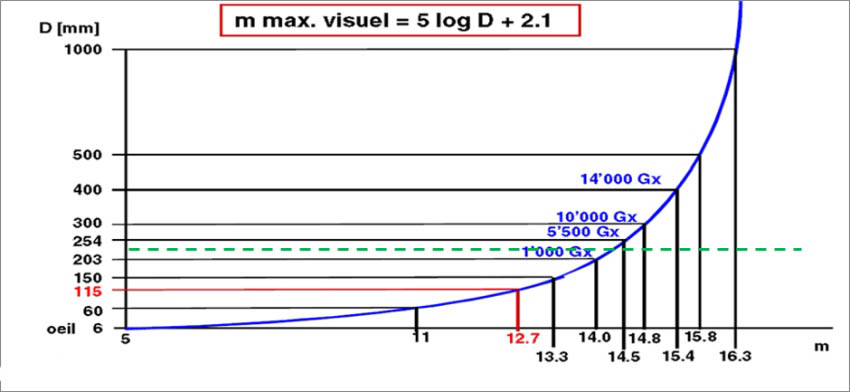
Le graphique ci-dessus indique la magnitude apparente limite en fonction du diamètre (D) de l’instrument d’observation utilisé. Le trait hachuré vert représente la limite de mon télescope de 203 mm utilisé en visuel. Nous verrons comment la photographie, exploitée avec un même instrument d’observation, permet de dépasser très sensiblement cette limite.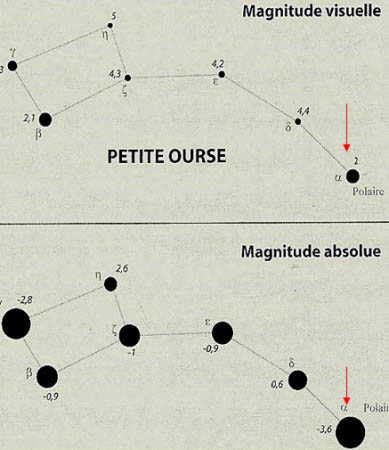
Les deux figures à gauche ci-contre montrent, pour la Petite Ourse, la différence entre le magnitude visuelle et la magnitude absolue de chaque étoile. On constate ainsi que l’étoile polaire est bien plus puissante qu’elle ne parait à l’observation.
Les astronomes ont eu besoin d’adopter une autre échelle nommée magnitude absolue (abréviation « M »), tenant compte des caractéristiques réelles, et non plus apparentes, des objets. Imaginons une étoile très puissante située à un telle distance que sa lumière nous parvienne à peine, sa magnitude apparente sera élevée alors que sa magnitude absolue sera faible. (attention à la confusion que peut induire l’échelle inversée des magnitudes, où plus l’objet est brillant, plus sa magnitude est faible et inversement).
Il existe aussi d’autres échelles: celle tenant compte du rayonnement stellaire sur la totalité du spectre lumineux se nomme magnitude bolométrique, ou celle qui en astrophotographie, prend en considération le spectre décelable par un capteur numérique, la magnitude photoélectrique.