Les distances en astronomie
Les unités de distance usuelles comme le mètre et le kilomètre ne sont plus adaptées lorsqu’on évoque les distances astronomiques. Il est très difficile de se représenter la distance qui nous sépare de l’étoile la plus proche de la Terre, Proxima du Centaure, qui se trouve à 40.000 milliards de km de nous. Pour explorer en profondeur l‘Univers, il faut s’adapter à cette contrainte et utiliser des unités spécifiques, l’astronome amateur utilise généralement l’année lumière, alors que les astronomes professionnels lui préfèrent le parsec.
 L’année lumière (abréviation: al) est la distance parcourue en une année julienne (365.25 jours) par la lumière (photon) dans le vide, en dehors de tout champ gravitationnel ou magnétique. Sa vitesse (nommée aussi célérité) étant de 299.792.458 km/s, une année-lumière est égale à : 9.460.730.472.580 km (9.460 milliards de km). Autrement dit la lumière se déplace à 1,08 milliards de km/heure.
L’année lumière (abréviation: al) est la distance parcourue en une année julienne (365.25 jours) par la lumière (photon) dans le vide, en dehors de tout champ gravitationnel ou magnétique. Sa vitesse (nommée aussi célérité) étant de 299.792.458 km/s, une année-lumière est égale à : 9.460.730.472.580 km (9.460 milliards de km). Autrement dit la lumière se déplace à 1,08 milliards de km/heure.
L’unité Astronomique (abréviation: ua) est la distance moyenne entre la Terre et le Soleil. Une « ua » vaut 149,6 millions de km. C’est pourtant une unité de faible valeur, utilisée essentiellement sur de petites distances comme par exemple celles mesurées au sein du système solaire.
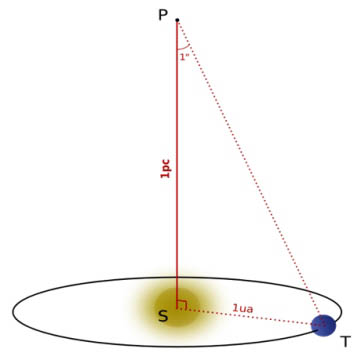
Le parsec (pc) est l’unité de longueur utilisée par les astronomes professionnels, sa valeur est égale à la distance à laquelle une unité astronomique sous-tend un angle d'une seconde d'arc (schéma ci-dessus). Un parsec équivaut à 3.26 al.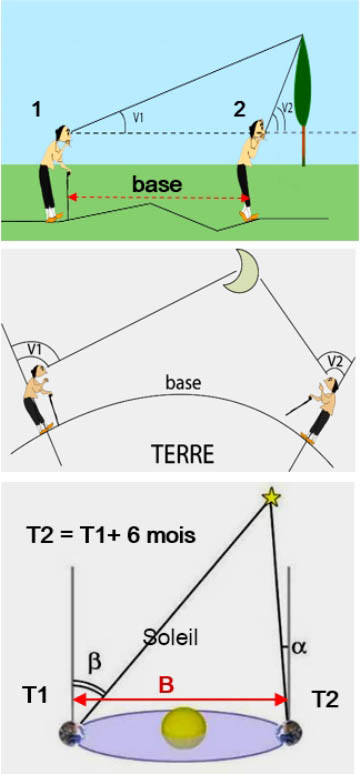 Sur Terre, pour mesurer la distance d’un objet on utilise la méthode de triangulation. Pour cela on vise l’objet (1), on se déplace d'une distance appelée base et on vise de nouveau l’objet (2). Dans le triangle Objet-Visée1-Visée 2, on connaît un côté (la base) et les angles V1 et V2, on peut alors calculer les autres côtés et déterminer la distance de l'objet. Cette méthode est appelé parallactique.
Sur Terre, pour mesurer la distance d’un objet on utilise la méthode de triangulation. Pour cela on vise l’objet (1), on se déplace d'une distance appelée base et on vise de nouveau l’objet (2). Dans le triangle Objet-Visée1-Visée 2, on connaît un côté (la base) et les angles V1 et V2, on peut alors calculer les autres côtés et déterminer la distance de l'objet. Cette méthode est appelé parallactique.
Pour calculer la distance d'un corps céleste à la Terre, on procède de la même manière en choisissant deux lieux sur Terre d’où on mesure l'angle de vue de l’objet. (fig.ci-contre à droite) Cette méthode a ses limites, car si l'astre est très loin, la plus grande base terrestre ne pouvant dépasser 12.000 km, la différence d'angle de visée entre les deux points d’observation sera infinitésimale et pas mesurable avec les instruments dont on dispose.
On procèdera alors à une triangulation particulière, nommée parallaxe annuelle (figure en bas à droite), mesurée à partir de deux positions orbitales distinctes de la Terre:
Pour mesurer les angles alpha et beta (équivalents des V1 et V2 du schéma précédents) avec une base suffisamment grande, on prend la base B résultant de deux positions extrêmes de la Terre sur son orbite autour du soleil (B = 300 millions de km à son maximum, correspondant au grand diamètre de l’ellipse de l’orbite terrestre).
Pour se ramener à une base de 1ua (soit B/2 sur la figure de droite) on doit prendre en compte la valeur angulaire résultant (alpha + béta)/2.
Ainsi si la parallaxe (p)mesurée (α+β)/2 = 3’’ d’arc, l'étoile est à une distance de 1/3 parsecs de la Terre ( d (en parsec) =1/p) .
Compte tenu de leur éloignement énorme par rapport à la dimension de la base, très peu d’étoiles cependant peuvent être mesurées depuis la Terre. De nos jours, des satellites astrométriques comme « Hipparcos » ou « Gaia » permettent d’augmenter la précision de mesure de la parallaxe et d'obtenir la distance à la Terre d’un plus grand nombre d'étoiles. Cependant, dans l'espace également ce mode de mesure trouve vite ses limites lorsqu'il s'agit d'objets trop lointains car les angles de parallaxes demeurent trop petits pour être différenciés. On a alors recours aux méthodes de l'astrophysique qui tirent profit de la différence de magnitudes, entre celle intrinsèque à l'objet et celle que l'on observe, ce qui est détaillé dans la seconde partie de l'ouvrage de Serge Rochain que je cite ci-après.
NB: Pour en savoir plus sur la mesure des distances, je recommande vivement le livre "Histoire de la mesure des distances cosmiques " écrit par Serge Rochain, diplômé de l'université de Paris XI en astronomie et astrophysique et avec qui je partage des missions d'observation sur le coronographe du Pic du Midi.
Vous pouvez également télécharger le PDF de l'article "Pour un parsec populaire" - ( Plaidoyer pour l'usage du parsec en public) écrit par Christophe Marty, astronome amateur à la "SAP" Société d'Astronomie Populaire de Toulouse.
