Les coniques
Il me semble utile de passer très sommairement en revue les différentes figures géométriques qui découlent de l’intersection d’un plan avec un cône de base circulaire. L’étude du mouvement des astres ne peut faire l’économie de cette partie de la géométrie qui fut remarquablement étudiée par les grecs anciens, notamment le géomètre et astronome grec Apollonius de Perge (245 av. J.-C.) à qui l’on doit les premiers théorèmes relatifs à ces figures que l’on nomme « sections coniques ».
De nombreux mathématiciens ont étudié ces figures dont les multiples propriétés furent exploitées par les géomètres, les architectes, les astronomes, les opticiens et même les jardiniers qui imaginèrent chacun des moyens techniques pour reproduire leurs différentes figures. Au XVIIème siècle, René Descartes mit en place les bases de la géométrie analytique, le terme de coniques cède alors sa place à celui de courbes du second degré. De son côté, Pascal travailla sur la géométrie pure pour mettre en place les fondements de l’étude projective des coniques. Ces sections coniques, ainsi définies par les grecs mettent en évidence différents types de courbes que l’on peut classer suivant quatre grandes familles:
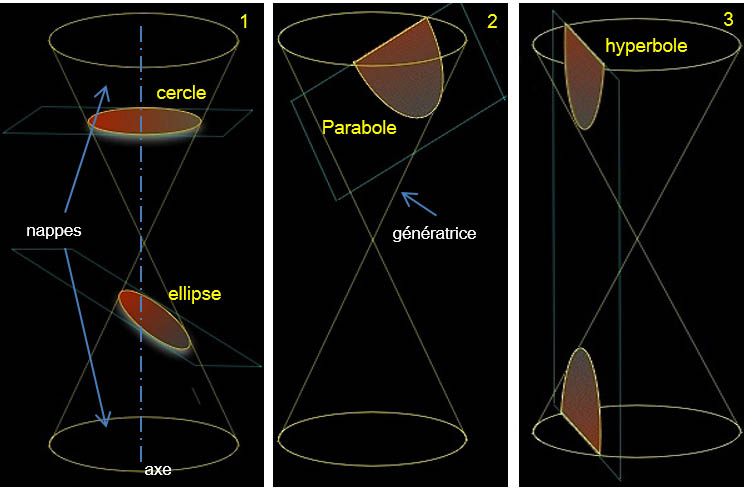
1) Le cercle: Résulte de l’intersection d’un plan perpendiculaire à l’axe d’un cône.
2) L’ellipse: Résulte de l’intersection d’un plan incliné par rapport à l’axe du cône.
3) La parabole: Résulte de l’intersection d’un plan parallèle à un plan tangent au cône.
4) L’hyperbole: Résulte de l’intersection d’un plan incliné ou parallèle à l’axe du cône.
Le cercle caractérisé par son centre et son rayon, fut par exemple utilisé pour la réalisation des sphères armillaires qui permettaient de représenter certains mouvements apparents des astres par le biais d’une modélisation de la sphère céleste. Ainsi Ptolémée parvint à déterminer l’heure de l’équinoxe en utilisant une sphère armillaire constituée de deux cercles perpendiculaires. Cette sphère également nommée astrolabe sphérique ne cessa d’être améliorée au cours des siècles. La découverte du mouvement orbital par Kepler fit de l’ellipse une des figures les plus étudiées en astronomie. En effet, tous les corps qui gravitent autour du Soleil: planètes, comètes, astéroïdes, etc.… possèdent une orbite elliptique. Cette figure est définie par ses deux foyers, son grand axe (distance maximale entre deux points d’une ellipse) et son excentricité « e » (chiffre entre 0 et 1 qui donne l’aplatissement de l’ellipse). Les trajectoires paraboliques ou hyperboliques sont des trajectoire elliptiques particulières: Si « e » = 0, la trajectoire est un cercle. Si 0<e <1, la trajectoire est une ellipse. Si e = 1, la trajectoire est une parabole et si e>1, la trajectoire est une hyperbole. Les relevés de positions d’objets célestes comparés aux équations de ces figures géométriques permettent ainsi de déduire la nature de leurs trajectoires. Les éventuelles anomalies constatées entre les relevés des astronomes et les équations définissant les positions ou mouvement théoriques des astres observés (tenant également compte des interactions gravitationnelles connues, comme la proximité d’autres planètes), ont permis par exemple de mettre en évidence la présence de corps célestes, sans même les avoir aperçus. Le cas le plus célèbre en astronomie, fut la découverte, grâce au seul calcul, de la planète Neptune par Urbain Le Verrier. Les calculs de trajectoires complexes et fastidieux imposaient aux astronomes d’interminables heures de travail dont ils s’acquittaient souvent en confiant ces corvées à leurs assistants. A cette occasion, nombre de femmes firent leur entrée dans une discipline auparavant réservée aux hommes.
