Le pendule
Depuis l’Antiquité, le pendule a intrigué plus d’un astronome. Instrument d’apparence rudimentaire, il accompagne le périple des hommes à la conquête du temps. J'ai évoqué dans des articles de ce site, les calendriers, les gnomons, les cadrans solaires, n’oublions pas non plus les sabliers et les clepsydres, premières horloges indépendantes des astres considérées comme déplaçables. Leur précision reste cependant trop aléatoire pour envisager d’effectuer des mesures physiques fiables, en particulier en astronomie. L’apparition d’horloges mécaniques révolutionne cet état de fait. Le pendule, de par ses propriétés y joue un rôle essentiel. Il a la particularité de permettre une division du temps en partie rigoureusement égales. Cette propriété, sera exploitée pour fabriquer des régulateurs dans les mécanismes horlogers des astronomes, jusqu’à l’apparition des horloges à quartz vers 1930.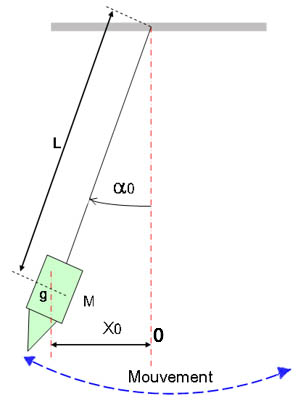 
Ci-contre, un pendule simple de masse M, de centre de gravité g, suspendu à un fil de longueur L est animé d’un mouvement dont l’écart de balancement est matérialisé par la distance X0 (correspondant à l’angle α0 mesuré entre le fil avec la position du pendule au repos). Sous l’effet de la pesanteur, le pendule va constamment tendre à être ramené vers sa position d'équilibre (au point 0). Il va osciller, chaque fois qu’il sera écarté de cette position. On peut imaginer que plusieurs paramètres agissent sur la durée de sa période. Par exemple, la masse M, l’écart de balancement X0, et la longueur L. Afin de vérifier l’influence de ces derniers, les astronomes et physiciens ont fait varier séparément chacun d’entre eux. Après avoir effectué ces expériences, Galilée découvrira que T= L/g, signifiant que la période du pendule ne dépend que de sa longueur et aucunement de sa masse. Concernant X0, il constate qu’elle n’a d’influence que sur l’amplitude du mouvement (distance), sans affecter sa période (temps).
Pour trouver une explication, les astronomes et physiciens font le bilan des forces qui s’exercent sur le pendule (schéma ci-dessous): Le poids P et la traction du fil T (ils négligent les frottements), puis ils font un bilan des énergies mécaniques* en présence:
E mécanique = E cinétique + E potentielle : Em = ½ ML²α0² + MgL(1-cosα0).
(g étant l’accélération due à la pesanteur, soit 9.81 m/s-2 à nos latitudes).
*De manière simple on peut dire que durant son mouvement , le pendule transforme alternativement énergie potentielle et énergie cinétique. L'énergie potentielle est maximale et l'énergie cinétique est nulle lorsque le pendule est en bout de course. (α0 maximal) tandis que lorsque α0 est = à zéro (position verticale) l'énergie cinétique est à son maximal et l'énergie potentielle à son minimum.
D’autres calculs très complexes seront nécessaires pour progresser dans la connaissance de ce mouvement, suivant différents cas de figure. C’est seulement au XIXème siècle que Jacobi, grâce à ses fonctions elliptiques, arrivera à en établir la formule générale.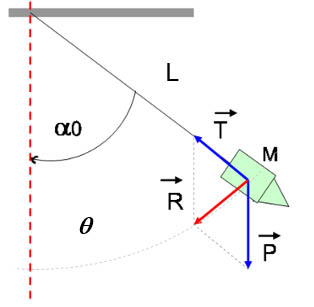
Même si les propriétés du pendule ne sont pas encore toutes démontrées mathématiquement au XVIIème siècle, certaines sont bien connues. L’approximation de la durée de la période d’un pendule simple de faible amplitude s’exprime déjà sous la forme:
T0 = 2 π x (l/g)-2 .
Elle permet de ne pas rester bloqué au niveau de son utilisation pour les mesures physiques.
Par exemple, lorsque les astronomes dotés de pendules ont commencé à effectuer des mesures en différents points de la Terre, ils ont constaté qu’ils devaient allonger ou raccourcir la valeur de L suivant les lieux où ils se trouvaient, afin de conserver une durée T constante. Il en déduisirent, que g variait et purent ainsi établir que la Terre n’était pas sphérique, mais légèrement aplatie à ses pôles. D’autres mesures furent entreprises sur la base du pendule et de nombreuses applications développées. Pour s’en convaincre on peut citer les différents pendules utilisés: pendules sphériques, coniques, de Foucault, balistiques, de torsion, de Newton, de Huygens, cycloïdaux, elliptiques, de Pohl, élastiques...
Remarque: Sans compter le pendule du radiesthésiste dont la singularité réside dans le fait qu’aucune équation ne saurait définir son mouvement. En revanche, ce même pendule, véritable aubaine pour nombre de charlatans, exploite à merveille la crédulité ou l'ignorance qui, elles aussi et je le déplore, me donnent parfois une idée de l'infini...