La réfraction
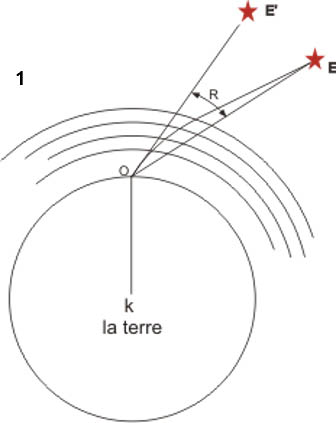La réfraction est une source d’erreur dans l'évaluation de la position angulaire réelle des objets célestes observés. Ce phénomène fait paraitre l’objet observé plus haut dans le ciel qu’il ne l’est en réalité. Le schéma ci-contre montre comment un observateur situé à la surface de la Terre verra une étoile en « E’ » au lieu de la voir en « E ». Les astronomes qui effectuent des mesures relatives aux positions des astres doivent donc effectuer une correction de cette différence de hauteur nommée réfraction atmosphérique. Les différentes strates de l’atmosphère ne produisent pas une réfractions uniforme entre les couches supérieures et les couches inférieures. On observe ainsi des variations sensibles, telles que les rayons lumineux issus d’un astre nous parviennent après un ou plusieurs changements de direction.
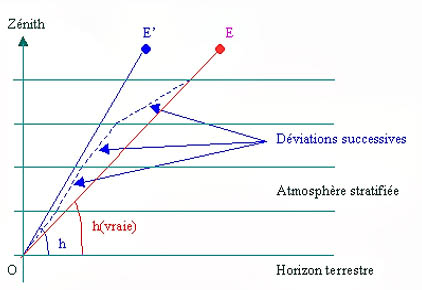La figure ci-contre à droite, tout comme le premier schéma (1), montrent que pour un observateur placé au point «O» l’astre positionné en «E» parait se trouver en « E’». La différence entre les deux figure réside dans le fait que la hauteur «h» apparente résulte d’une trajectoire incurvée de la lumière, dont la concavité est orienté vers la Terre.
Les facteurs intervenant sur la valeur de la réfraction dépendent essentiellement de la température de l’air et de la pression barométrique.
De manière générale, lorsqu’un astronome prend en compte la réfraction, il corrige ses relevés de la valeur moyenne de celle-ci. La réfraction peut être importante pour un objet situé à proximité de l'horizon terrestre, par exemple elle atteint 36'36'' à H0=0° .
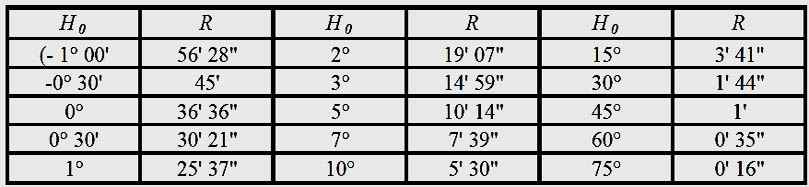
Le tableau ci-dessus, issu des tables éphémérides, met en évidence le fait que la réfraction s'amenuise à mesure que la position de l’objet observé s'élève dans le ciel (valeur Ho du tableau), pour finalement se révéler inexistante à l'approche de la direction zénithale (Ho=90°). Il en résulte l’introduction d’une correction dans le calcul théorique des coordonnées horizontales locales (azimut et hauteur) de l'objet observé. La valeur du coefficient de réfraction s’établit donc à partir de la formule :
R(h) = h-hvraie
Une fois cette première approche effectuée, on doit également prendre en compte le fait que la réfraction atmosphérique qui se rapporte à un objet dépend également du lieu d’observation. Les mesures on permit d’établir que la variation de la réfraction est impactée en raison inverse de l'accroissement d’altitude de ce lieu d’observation. En effet, toutes choses égales par ailleurs, plus un lieu d’observation sera élevé, moins la pression atmosphérique y sera forte, mais il s'avère qu'on doit également prendre en compte la température de ce lieu.
Il convient donc d’appliquer à la réfraction relative à la valeur angulaire de l’objet observé, une correction qui dépend de ces deux paramètres (pression/température) relevés sur le lieu d’observation. Pour cela, on pourra utiliser la formule proposée par l’astronome Jean Meeus :
Coeff = (P/1010)x(283/(273+T) , dans laquelle P est exprimé en hPa et T en °C.
NB : A titre indicatif on peut consulter les tableaux suivants : « pression/altitude » et « température /altitude ».
Exemple : Si on se situe à 1000 m d’altitude avec une pression barométrique de 896 hPa, une température de 8°C et que l’objet visé se situe à 10° de l’horizon, on pourra, à partir de la réfraction donnée par le tableau ci-dessus (soit 5’30’’) appliquer le coefficient de correction : (896/1010) x (283/(273+8) = 0.8871x1,0071 = 0.8934
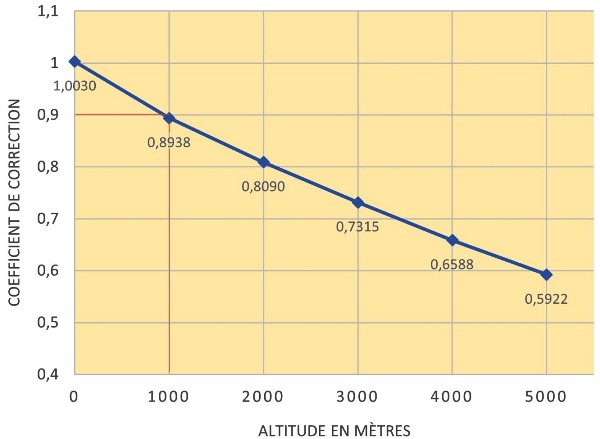En revanche, lorsque l’observateur ignore la pression atmosphérique et la température du lieu d’observation, il peut se servir d'un graphique tel que celui proposé ci-contre (dont la courbe est établie pour les valeurs conventionnelles de T et P, soit respectivement 10°C et 1013 hPa). Il lui suffit alors de multiplier la réfraction calculée dans un premier temps selon la position angulaire de l’objet observé par le coefficient qui apparait ici sur l'axe des ordonnées (l'altitude du lieu d'observation étant indiquée en abscisse).
Remarque : Les calculs théoriques relatifs à la réfraction sont très complexes et font intervenir une multitude de paramètres qui vont bien au-delà d’un angle, d’une température et d’une pression barométrique. ( voir : https://fr.wikipedia.org/wiki/Indice_de_r%C3%A9fraction ). Cependant, si on raisonne en ordre de grandeur, les valeurs aproximative données par la formule de Meeus restent satisfaisantes pour l’observation courante.