La gravitation
Lorsqu’un objet chute, il est animé par une force le poussant du haut vers le bas. Cette force est appelée force de gravitation. On a l’habitude de dire que si un objet tombe, c’est parce qu’il a un certain poids. Sur Terre, le poids d'un corps tombant au sol correspond en réalité à la force qu'exerce sur ce corps, le champ gravitationnel terrestre. Cette force peut varier en fonction, par exemple, de l’altitude, ce qui permet de constater que le poids n’est donc pas une valeur fixe. Pour bien comprendre le principe de la gravitation découvert par Isaac Newton, il faut faire appel à la notion de masse:
La masse étant une caractéristique propre à la quantité de matière d’un corps donné, alors que le poids dépend de la force de gravitation à laquelle cette masse (ce corps) est soumise; la relation entre la masse et le poids est donnée par l'équation : P=mg (ou m=P/g), dans laquelle P représente le poids (en newtons), m la masse (en kg) et g l'intensité locale du champ gravitationnel (en Newton/kg). Sur la Terre, au niveau de la mer "g" a une valeur de 9.81 Newton/kg (on peut remarque que la même mesure effectuée au sommet de l'Everest donnerait à "g" une valeur de 9.78 N/kg). Le poids est donc proportionnel à la masse d’un corps et à la force de gravitation s’exerçant sur lui. Isaac Newton a découvert que: « Deux corps quelconques s'attirent en raison directe de leur masse et en raison inverse du carré de la distance séparant leurs centres de gravité »
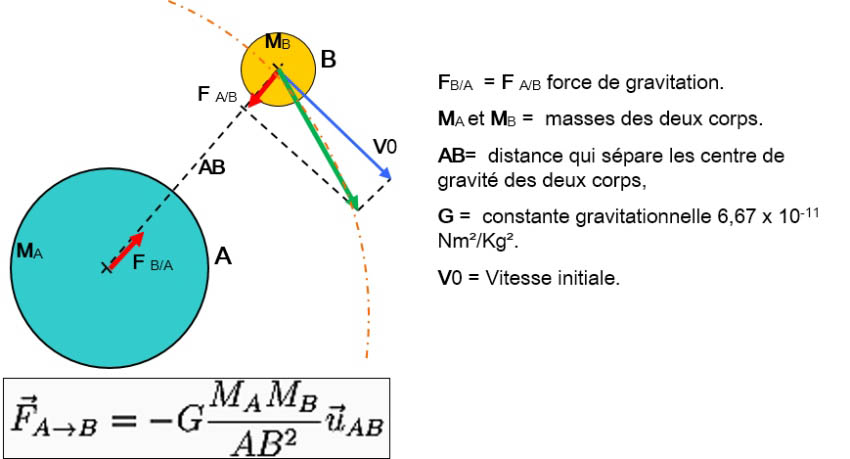
Dans l'exemple ci-dessus, qui pourrait illustrer celui de la Lune et de la Terre, on note V0 (bleu) qui représente la vitesse à laquelle la Lune tourne autour de la Terre. Et FA/B (rouge) représentant l’attraction qu’exerce le corps A (Terre) sur le corps B (la Lune). Si on trace la résultante des deux vecteurs (vitesse V0) et force de gravitation (FA/B), On remarque que le vecteur obtenu (vert) reste positionné sur l’orbite décrite par B (pointillés orange) et de ce fait maintient en équilibre les 2 forces V0 et FA/B.
F B/A = F A/B force de gravitation.
MA et MB = masses des deux corps.
AB= distance qui sépare les centre de gravité des deux corps,
G = constante gravitationnelle 6,67 x 10-11 Nm²/Kg².
V0 = Vitesse initiale.
C’est grâce à cet équilibre que la Lune reste en orbite autour de la Terre et la Terre autour du Soleil. Cette loi s’applique généralement à la totalité des corps évoluant dans notre système. Concernant les corps évoluant aux limites de l’univers, la notion d’espace temps vient impacter cette loi de Newton qui devient alors incomplète. Cependant, appliquée au objets célestes visibles, elle nous permet de déterminer leurs trajectoires de manière satisfaisante.
Cette loi, généralisée à un nombre quelconque d'objets est suffisante pour retrouver avec une précision élevée la plupart des trajectoires d’objets célestes. Elle explique aussi bien, pourquoi la pomme tombe du pommier, que le mouvements des planètes, des comètes, et des astéroïdes dans le système solaire, ainsi que le mouvement de planètes gravitant autour d’autres étoiles, le mouvement des étoiles doubles ou multiples, la dynamique des amas stellaires, la condensation des nébuleuses, etc.
La force de gravitation est ainsi responsable de plusieurs manifestations naturelles : les marées, l'orbite des planètes autour du Soleil, la relative sphéricité de la plupart des corps célestes, etc... D'une manière plus générale, la structure à grande échelle de l'univers est déterminée elle aussi par la gravitation. Cette loi de Newton a été reprise en 1915 par Einstein qui a pu établir une théorie de la relativité générale. Cette dernière n’étant en définitive qu’une théorie « modernisée » de la gravitation.
