Effet Doppler-Fizeau

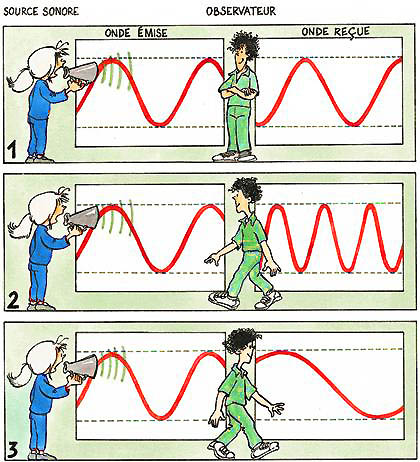Nous avons tous observé l’effet Doppler La sirène d’une ambulance qui s’approche émet un son aigu, qui, lorsqu’elle s’éloigne, devient grave. En 1842, Christian Doppler étudia ce phénomène et en déduisit que les ondes émises par une source mobile sont comprimées en avant de cette source et étirées en arrière. Ceci s’explique par le fait que la source rattrape les ondes devant, alors qu’elle s’en éloigne derrière. Doppler suggéra que les différences de couleurs des étoiles pourraient être dues à ce même effet, affectant leur lumière suivant le même principe que celui qu’il avait établi pour les ondes sonores.
En 1848, le français Fizeau montra que la vitesse des étoiles était trop faible par rapport à la vitesse de la lumière pour provoquer une modification significative de leurs couleurs. Il découvrit par contre que l’on pouvait détecter de faibles variations de la longueur d’onde de leurs raies spectrales. L’expérience fut réalisée en 1868 par l’anglais Huggins qui mesura le décalage des raies d’hydrogène dans le spectre de l’étoile Sirius et en déduisit qu’elle s’éloigne de nous à la vitesse de 45 Km/s. Cette vitesse de rapprochement ou d’éloignement se nomme vitesse radiale.
Principe de la vélocimétrie Doppler: Plus un corps se rapproche, plus la lumière qu'il émet se décale vers le bleu.  Plus il s'éloigne, plus sa lumière tire vers le rouge.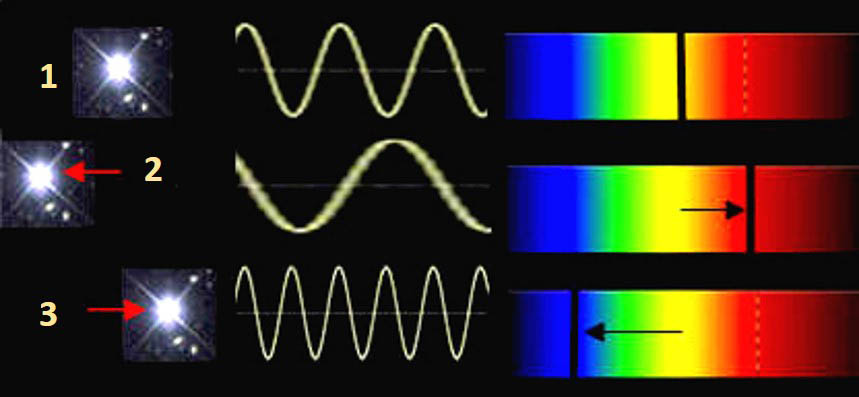
La vitesse radiale (VR) correspond à la vitesse d'un objet dans la direction de la ligne de vue. Elles caractérise en astronomie la vitesse à laquelle les objets célestes s’éloignent ou se rapprochent de nous. Une vitesse radiale positive indique que l’objet s’éloigne et une vitesse radiale négative qu’il se rapproche. La lumière d’un objet céleste qui possède une vitesse radiale significative est sujette à l'effet Doppler. Sa longueur d'onde augmentera si l'objet s'éloigne (cas n°2 ci-dessus) et diminuera s'il se rapproche (cas n°3 ci-dessus) si l'objet est fixe aucun décalage n'est observable (cas n°1).
La vitesse radiale d'une étoile, d'une galaxie ou d’un amas peut ainsi être évaluée à partir de l’analyse de son spectre lumineux. On compare, en laboratoire, les longueurs d’onde des raies de ce spectre avec des longueurs d'onde de raies spectrales connues. L’étude des vitesses radiales sert à déterminer la masse et certains éléments orbitaux des étoiles permettant notamment de détecter les exoplanètes.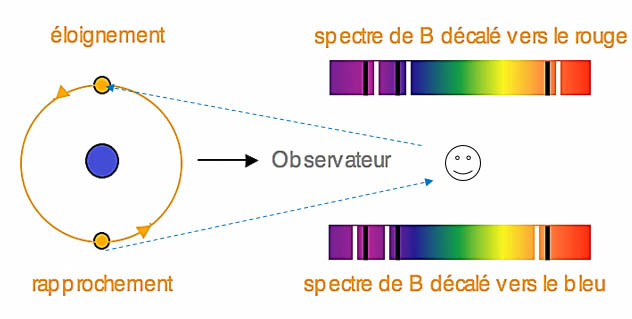

Une binaire spectroscopique est une étoile binaire dont le mouvement orbital (flèche circulaire orange) est mis en évidence par la variation de la vitesse radiale d'une ou des deux composantes du système. En effet lorsque l’étoile est dans la position « éloignement », comme le montre le schéma ci-contre, le spectre de sa lumière se trouve décalé vers le rouge. Lorsqu’elle se rapproche de nous son spectre se décale vers le bleu. Cette variation peut se mesurer à l’aide d’un spectrographe, en observant le déplacement par effet Doppler-Fizeau des raies spectrales de l'étoile, dû à sa vitesse orbitale le long de la ligne de visée. Les progrès des instruments permettent aujourd’hui de déceler des vitesses radiales de l’ordre du mètre/seconde et de mesurer d’infimes perturbations, dues par exemple à des compagnons planétaires et non plus seulement stellaires. C’est grâce à cette méthode que les astronomes ont pu découvrir la plupart des planètes extrasolaires connues.

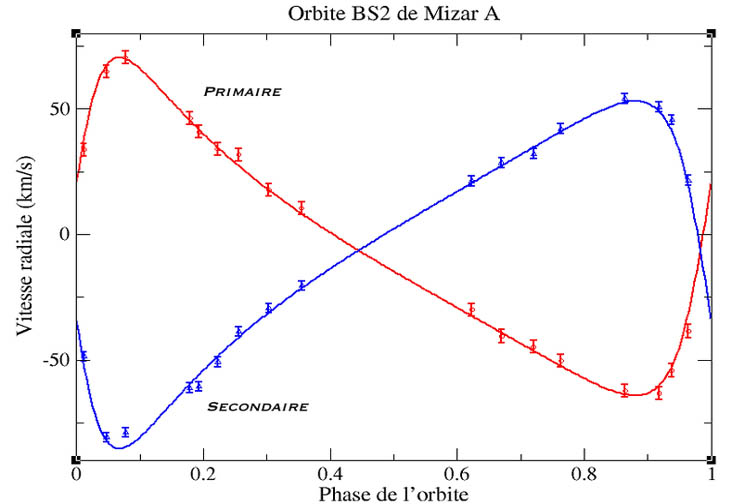Prenons l’exemple de Mizar de la Grande Ourse. C’est une binaire visuelle, dont chacune des composantes, Mizar A et Mizar B sont elles-mêmes des binaires spectroscopiques, ce qui en fait une étoile quadruple. On voit sur la figure de droite la courbe des variations de vitesse radiale de BS2 (Binaire Spectroscopique 2) dont la période est d’une vingtaine de jour. Ci dessous, on peut également voir le spectre de Saturne pris en positionnant la fente prés de son équateur. Ici apparait la raie H alpha issue de la réflexion de la lumière solaire. On peut constater qu’elle est inclinée par l’effet Doppler, du à la vitesse de rotation de Saturne sur elle-même. Des mesures précises de cet inclinaison permettront avec quelques équations de calculer la vitesse rotation de la planète.
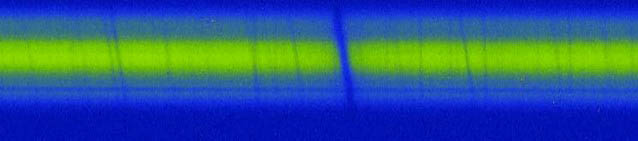Il est bien évident que le petit spectrographe «basique» réalisé par un amateur et constitué en partie d’éléments optiques de récupération assemblés et alignés avec les moyens du bord, ne saura pas à priori mesurer efficacement ce type de variation. Cependant les traitements numériques d’image associés à des logiciels de spectrographie, semblent faire reculer les limites de cette discipline et laissent envisager la possibilité d’utiliser des spectrographes abordables pour obtenir des résultats présentant un réel intérêt scientifique.

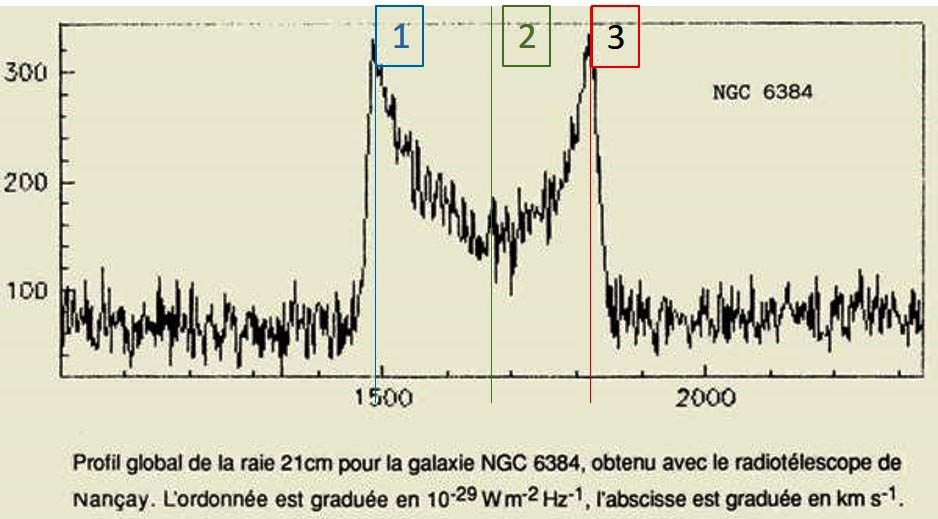Une autre application non négligeable de l'effet Doppler-Fizeau nous permet d'approcher la constante de Hubble* par la mesure de fuite des galaxies (en abscisse sur le diagramme ) avec le différentiel de la position de la raie 21 cm de l’hydrogène entre les mesures faites sur les bords opposés d’une galaxie (ici la galaxie spirale NGC 6384 ) vue par la tranche, comme le montre le schéma ci contre à gauche.  (1=Vitesse minimum / 2 =Vitesse globale de fuite ** /3 =Vitesse maximum***) .

Les différences entre les vitesses minimum et maximum sont dues à la rotation propre de la Galaxie qui pour un observateur distant, fait apparaître une vitesse apparente différente selon que la mesure soit effectuée sur un bord ou sur le bord opposé de la galaxie.

* La constante de Hubble (H₀) ( du nom de l'astronome Edwin Hubble qui fut le premier à la mettre en évidence) est le nom donné, en cosmologie, à la constante de proportionnalité qui existe entre la distance et la vitesse de récession apparente des galaxies dans l'univers observable. Elle est définie par la loi de Hubble qui donne le taux d'expansion actuel de l'Univers. Bien que dénommée «constante», ce paramètre cosmologique varie en fonction du temps et de ce fait décrit donc un taux d'expansion de l'univers. 

Remarque importante: En fait "H₀" désigne le taux d’expansion non pas à un instant donné mais par « bloc de distances », en l’occurrence 1 méga parsec à l’intérieur duquel il est considéré comme constant. Comme chaque bloc d’un mégaparsec se déplace en «s’appuyant» sur le bloc précédent, l’effet correspond pour un point donné à une accélération par rapport à un point origine situé hors du bloc et plus ce point est éloigné, plus le point observé semble accélérer. Aujourd’hui on pense que H₀ accélère, (La valeur actuellement admise de la constante de Hubble se situe  à 70 km/Sec/mégaparsec ) mais ce n’est qu’une découverte récente (2013) , car l’application de H₀ donne des distances moindres que les distances d’observation pour certains objets éloignés dont nous pouvons déterminer la distance de façon quasi certaine. En revanche, il semblerait qu'à ce jour, aucune théorie ne soit en mesure de dire si H a varié dans le passé, en dehors de la phase d’inflation qui aurait suivi de près le Bigbang.

** Cette valeur "2" ne donne pas directement la vitesse de fuite, elle donne la vitesse de fuite de la galaxie à la distance ou elle se trouve. Même si c’est une donnée qui intervient dans le calcul de H celle est loin d’être suffisante pour sa détermination.

***  Cette mesure met en évidence que les disques galactiques ne tournent pas à la vitesse où il devraient tourner en fonction de la distance au centre, selon la troisième loi de Kepler, avec un ralentissement proportionné à la racine carré du cube de la distance au centre. Ce rapport ne s’observe que sur une faible partie du rayon du disque depuis le centre. Au-delà le ralentissement et moindre et semble seulement linéaire.

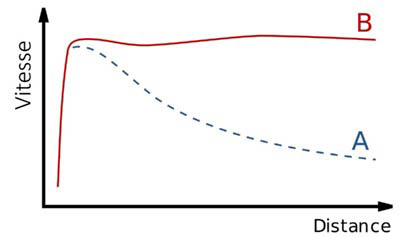L'application de la troisième loi de Kepler permet de visualiser ce ralentissement sur une courbe:

A :  courbe issue des calculs effectués sur la base de la  3^ème loi de Kepler.

B : courbe découlant de l'observation. Tournant trop vite, les étoiles en bordure du disque devraient être éjectées par centrifugation mais ce n’est pas le cas (De là l’hypothèse émise qu’une matière invisible viendrait augmenter la masse de la galaxie accroissant suffisamment sa gravité pour les retenir ?)

Exemple de calcul type :  Pour simplifier à outrance, considérons un modèle de galaxie spirale "théorique" dans laquelle les étoiles décriraient une orbite circulaire autour du centre galactique.
Et supposons que l’étoile située à 1 parsec (pc) du centre galactique mette 1000 ans (ma) pour parcourir la totalité de son orbite képlérienne. Selon Kepler : ( rappel:  (D/2)³ =  t² = constante).

Nous avons donc: ma = √1 pc³. La longueur de l’orbite est 2π (1pc) et la vitesse de l’étoile 2π/1000 = 6,28 c'est-à-dire 6,28 pc par période de 1000 ans.
L’étoile située à 2 pc du centre mettra donc √ 2pc³ = 2,82 ma pour parcourir son orbite. La taille de l’orbite est 4π (pc) et la vitesse de l’étoile 4π/2,82 ma = 4,45 pc/ma.
L’étoile située à 3 pc du centre mettra donc √ 3pc³ = 5,2 ma pour parcourir son orbite. La taille de l’orbite est 6π (pc) et la vitesse de l’étoile 6π/5,2 ma = 3,62 pc/ma.
L’étoile située à 4 pc du centre mettra donc √ 4pc³= 8 ma pour parcourir son orbite. La taille de l’orbite est 8π (pc) et la vitesse de l’étoile 8π/8 ma = 3,14 pc/ma.
On voit que conformément à la loi de Kepler la vitesse orbitale des étoiles diminue lorsque s'accroit la distance qui les sépare du centre galactique. Ainsi une étoile située à 10pc ne serait plus que 1,98 pc/ma.
La relation générale liant la vitesse orbitale d’une étoile à une distance D du centre galactique est donc 2Dπ /√D³.
Cette décroissance de la vitesse des étoiles est bien ce qui est observé pour les étoiles proches du centre galactique. En continuant, vers l’extérieur, sur une faible distance, les étoiles semblent de plus en plus rapides par rapport à l’estimation donnée par la 3^ème loi de Kepler, puis rapidement, elles tendent vers une vitesse uniforme qui devrait les éjecter de la galaxie à la distance où elle se trouvent car l’attraction diminue avec l’éloignement et seul une faible vitesse centrifuge permet de l’équilibrer.